Dijksitra算法求最短路仅仅适用于不存在右边是负权的情况(Bellman-Ford算法没有这一个限制)。主要特点是从起点为中心向外层层扩展,直到扩展到终点为止。
最短路的最优子结构性质
即一个最短路路径中经过的所有点这条路均是其最短路。(反证法易证)
Dijkstra基本思路:
①找到最短距离已经确定的顶点,从它出发更新相邻顶点的最短距离
②此后不需要再关心1中的”最短距离已经确定的顶点”
在最开始的时候,只有起点的最短距离是确定的。而在尚未使用过的顶点中,距离d[i]最小的顶点就是最短距离已经确定的顶点。由于不存在负边,所以d[i]不会再之后的更新中变小。这就是Dijkstra算法。
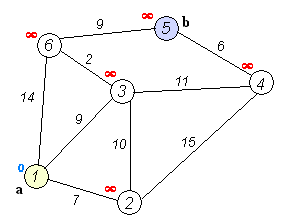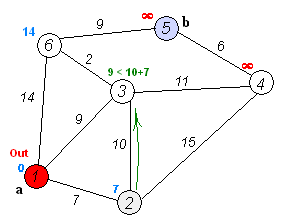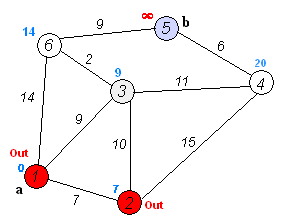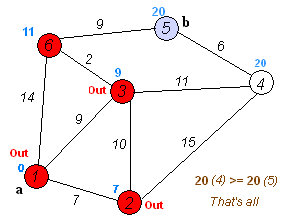
未优化的Dijkstra算法代码 int cost[max_v][max_v]; //使用邻接矩阵储存边(不存在就是INF)
int d[max_v]; //最短距离
bool used[max_v]; //已经确定最短路的图
int V;
//Dijkstra算法
void dijkstra(int s)
{
//初始化
fill(d,d+V,INF);
fill(used,used+V,false);
d[s] = 0;
//最短路
while(true) {
int v = -1;
for(int i = 0 ; i < V ; i ++) {
if(!used[i]) {
if(v == -1 || d[i] < d[v]) v = i;
}
}
if(v == -1) break;//如果都确定了就退出
used[v] = true;
for(int i = 0 ; i < V ; i ++) {
d[i] = min(d[i],d[v]+cost[v][i]);
}
}
}
使用优先队列优化代码
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
struct edge{int to,cost;};
typedef pair<int,int> P; //first是最短距离 second是顶点编号
int V;
vector<edge> G[max_v];//邻接表
int d[max_v];
void dijkstra(int s)
{
//通过指定greater<P>参数,堆按照first从小到大的顺序取出值
priority_queue<P,vector<P>,greater<P>> que;
fill(d,d+V,INF);
d[s] = 0;
que.push(P(0,s));
while(!que.empty()) {
P p = que.top();
que.pop();
int v = p.second;//编号
if(d[v] < p.first) continue;
for(int i = 0 ; i < G[v].size() ; i ++) {
edge e = G[v][i];
if(d[e.to] > d[v]+e.cost) {
d[e.to] = d[v]+e.cost;
que.push(P(d[e.to],e.to));
}
}
}
} Dijkstra算法的复杂度是O(|E|log|V|),可以更加高效求解最短路。但如果有负边还是要用Bellman-Ford算法。
