过拟合问题实战
1.构建数据集
我们使用的数据集样本特性向量长度为 2,标签为 0 或 1,分别代表了 2 种类别。借助于 scikit-learn 库中提供的 make_moons 工具我们可以生成任意多数据的训练集。
import matplotlib.pyplot as plt # 导入数据集生成工具 import numpy as np import seaborn as sns from sklearn.datasets import make_moons from sklearn.model_selection import train_test_split from tensorflow.keras import layers, Sequential, regularizers from mpl_toolkits.mplot3d import Axes3D
为了演示过拟合现象,我们只采样了 1000 个样本数据,同时添加标准差为 0.25 的高斯噪声数据:
def load_dataset(): # 采样点数 N_SAMPLES = 1000 # 测试数量比率 TEST_SIZE = None # 从 moon 分布中随机采样 1000 个点,并切分为训练集-测试集 X, y = make_moons(n_samples=N_SAMPLES, noise=0.25, random_state=100) X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=TEST_SIZE, random_state=42) return X, y, X_train, X_test, y_train, y_test
make_plot 函数可以方便地根据样本的坐标 X 和样本的标签 y 绘制出数据的分布图:
def make_plot(X, y, plot_name, file_name, XX=None, YY=None, preds=None, dark=False, output_dir=OUTPUT_DIR):
# 绘制数据集的分布, X 为 2D 坐标, y 为数据点的标签
if dark:
plt.style.use('dark_background')
else:
sns.set_style("whitegrid")
axes = plt.gca()
axes.set_xlim([-2, 3])
axes.set_ylim([-1.5, 2])
axes.set(xlabel="$x_1$", ylabel="$x_2$")
plt.title(plot_name, fontsize=20, fontproperties='SimHei')
plt.subplots_adjust(left=0.20)
plt.subplots_adjust(right=0.80)
if XX is not None and YY is not None and preds is not None:
plt.contourf(XX, YY, preds.reshape(XX.shape), 25, alpha=0.08, cmap=plt.cm.Spectral)
plt.contour(XX, YY, preds.reshape(XX.shape), levels=[.5], cmap="Greys", vmin=0, vmax=.6)
# 绘制散点图,根据标签区分颜色m=markers
markers = ['o' if i == 1 else 's' for i in y.ravel()]
mscatter(X[:, 0], X[:, 1], c=y.ravel(), s=20, cmap=plt.cm.Spectral, edgecolors='none', m=markers, ax=axes)
# 保存矢量图
plt.savefig(output_dir + '/' + file_name)
plt.close()
def mscatter(x, y, ax=None, m=None, **kw):
import matplotlib.markers as mmarkers
if not ax: ax = plt.gca()
sc = ax.scatter(x, y, **kw)
if (m is not None) and (len(m) == len(x)):
paths = []
for marker in m:
if isinstance(marker, mmarkers.MarkerStyle):
marker_obj = marker
else:
marker_obj = mmarkers.MarkerStyle(marker)
path = marker_obj.get_path().transformed(
marker_obj.get_transform())
paths.append(path)
sc.set_paths(paths)
return sc
X, y, X_train, X_test, y_train, y_test = load_dataset() make_plot(X,y,"haha",'月牙形状二分类数据集分布.svg')
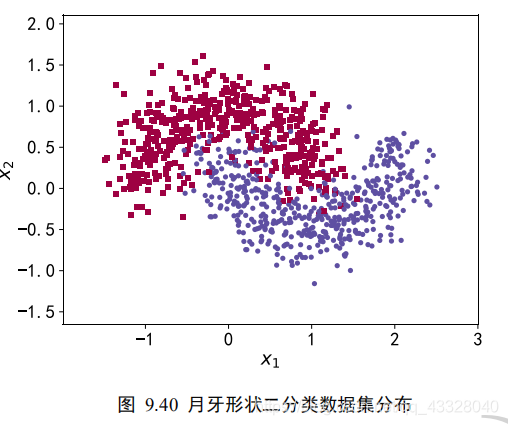
2.网络层数的影响
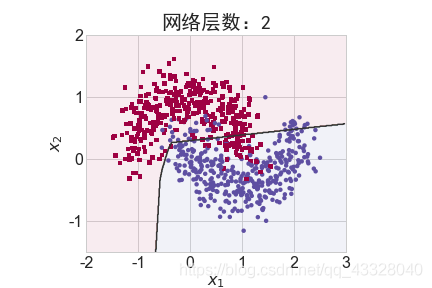
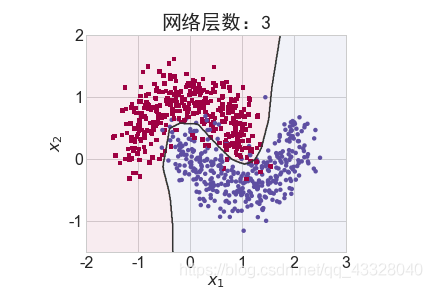
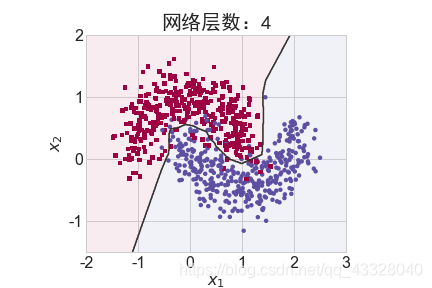
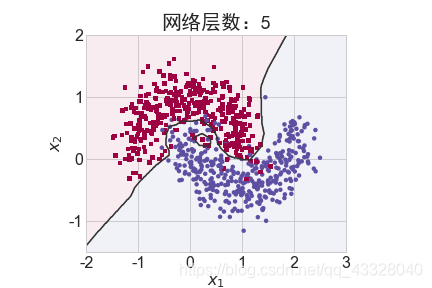
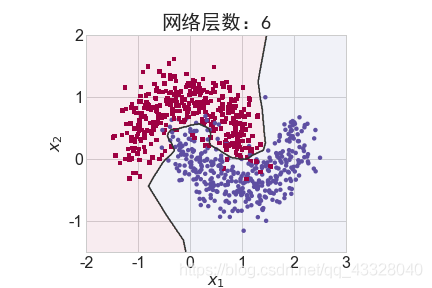
为了探讨不同的网络深度下的过拟合程度,我们共进行了 5 次训练实验。在𝑛 ∈ [0,4]时,构建网络层数为n + 2层的全连接层网络,并通过 Adam 优化器训练 500 个 Epoch
def network_layers_influence(X_train, y_train):
# 构建 5 种不同层数的网络
for n in range(5):
# 创建容器
model = Sequential()
# 创建第一层
model.add(layers.Dense(8, input_dim=2, activation='relu'))
# 添加 n 层,共 n+2 层
for _ in range(n):
model.add(layers.Dense(32, activation='relu'))
# 创建最末层
model.add(layers.Dense(1, activation='sigmoid'))
# 模型装配与训练
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
model.fit(X_train, y_train, epochs=N_EPOCHS, verbose=1)
# 绘制不同层数的网络决策边界曲线
# 可视化的 x 坐标范围为[-2, 3]
xx = np.arange(-2, 3, 0.01)
# 可视化的 y 坐标范围为[-1.5, 2]
yy = np.arange(-1.5, 2, 0.01)
# 生成 x-y 平面采样网格点,方便可视化
XX, YY = np.meshgrid(xx, yy)
preds = model.predict_classes(np.c_[XX.ravel(), YY.ravel()])
print(preds)
title = "网络层数:{0}".format(2 + n)
file = "网络容量_%i.png" % (2 + n)
make_plot(X_train, y_train, title, file, XX, YY, preds, output_dir=OUTPUT_DIR + '/network_layers')
3.Dropout的影响
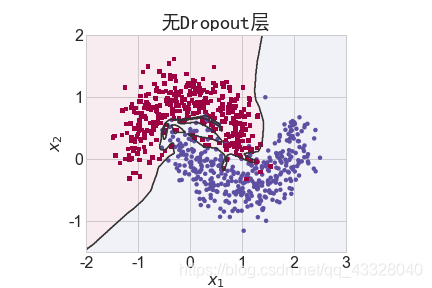
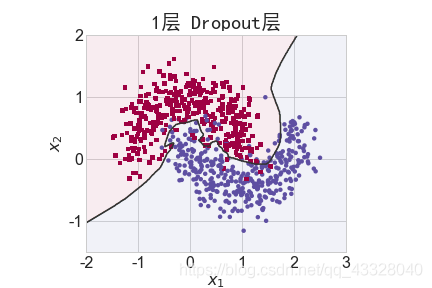
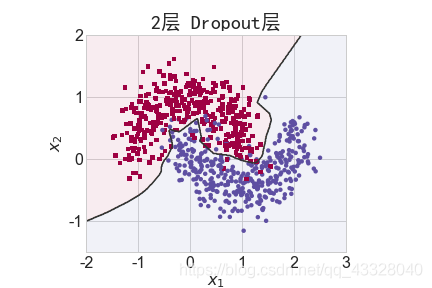
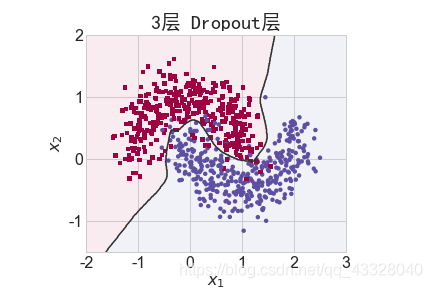
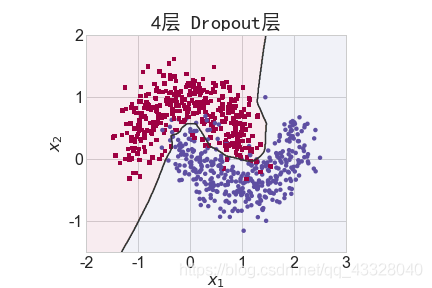
为了探讨 Dropout 层对网络训练的影响,我们共进行了 5 次实验,每次实验使用 7 层的全连接层网络进行训练,但是在全连接层中间隔插入 0~4 个 Dropout 层并通过 Adam优化器训练 500 个 Epoch
def dropout_influence(X_train, y_train):
# 构建 5 种不同数量 Dropout 层的网络
for n in range(5):
# 创建容器
model = Sequential()
# 创建第一层
model.add(layers.Dense(8, input_dim=2, activation='relu'))
counter = 0
# 网络层数固定为 5
for _ in range(5):
model.add(layers.Dense(64, activation='relu'))
# 添加 n 个 Dropout 层
if counter < n:
counter += 1
model.add(layers.Dropout(rate=0.5))
# 输出层
model.add(layers.Dense(1, activation='sigmoid'))
# 模型装配
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
# 训练
model.fit(X_train, y_train, epochs=N_EPOCHS, verbose=1)
# 绘制不同 Dropout 层数的决策边界曲线
# 可视化的 x 坐标范围为[-2, 3]
xx = np.arange(-2, 3, 0.01)
# 可视化的 y 坐标范围为[-1.5, 2]
yy = np.arange(-1.5, 2, 0.01)
# 生成 x-y 平面采样网格点,方便可视化
XX, YY = np.meshgrid(xx, yy)
preds = model.predict_classes(np.c_[XX.ravel(), YY.ravel()])
title = "无Dropout层" if n == 0 else "{0}层 Dropout层".format(n)
file = "Dropout_%i.png" % n
make_plot(X_train, y_train, title, file, XX, YY, preds, output_dir=OUTPUT_DIR + '/dropout')
4.正则化的影响
为了探讨正则化系数𝜆对网络模型训练的影响,我们采用 L2 正则化方式,构建了 5 层的神经网络,其中第 2,3,4 层神经网络层的权值张量 W 均添加 L2 正则化约束项:
def build_model_with_regularization(_lambda): # 创建带正则化项的神经网络 model = Sequential() model.add(layers.Dense(8, input_dim=2, activation='relu')) # 不带正则化项 # 2-4层均是带 L2 正则化项 model.add(layers.Dense(256, activation='relu', kernel_regularizer=regularizers.l2(_lambda))) model.add(layers.Dense(256, activation='relu', kernel_regularizer=regularizers.l2(_lambda))) model.add(layers.Dense(256, activation='relu', kernel_regularizer=regularizers.l2(_lambda))) # 输出层 model.add(layers.Dense(1, activation='sigmoid')) model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy']) # 模型装配 return model
下面我们首先来实现一个权重可视化的函数
def plot_weights_matrix(model, layer_index, plot_name, file_name, output_dir=OUTPUT_DIR):
# 绘制权值范围函数
# 提取指定层的权值矩阵
weights = model.layers[layer_index].get_weights()[0]
shape = weights.shape
# 生成和权值矩阵等大小的网格坐标
X = np.array(range(shape[1]))
Y = np.array(range(shape[0]))
X, Y = np.meshgrid(X, Y)
# 绘制3D图
fig = plt.figure()
ax = fig.gca(projection='3d')
ax.xaxis.set_pane_color((1.0, 1.0, 1.0, 0.0))
ax.yaxis.set_pane_color((1.0, 1.0, 1.0, 0.0))
ax.zaxis.set_pane_color((1.0, 1.0, 1.0, 0.0))
plt.title(plot_name, fontsize=20, fontproperties='SimHei')
# 绘制权值矩阵范围
ax.plot_surface(X, Y, weights, cmap=plt.get_cmap('rainbow'), linewidth=0)
# 设置坐标轴名
ax.set_xlabel('网格x坐标', fontsize=16, rotation=0, fontproperties='SimHei')
ax.set_ylabel('网格y坐标', fontsize=16, rotation=0, fontproperties='SimHei')
ax.set_zlabel('权值', fontsize=16, rotation=90, fontproperties='SimHei')
# 保存矩阵范围图
plt.savefig(output_dir + "/" + file_name + ".svg")
plt.close(fig)
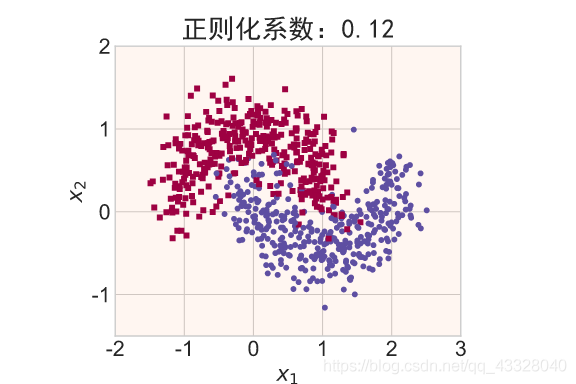
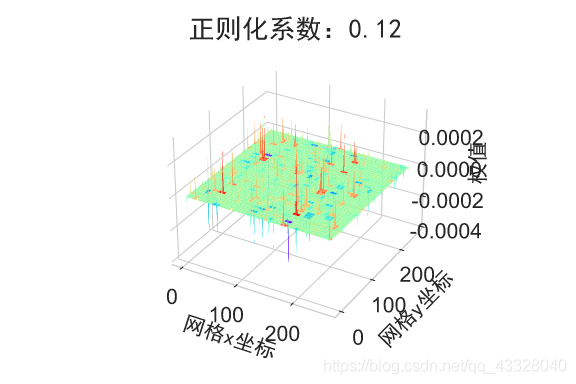
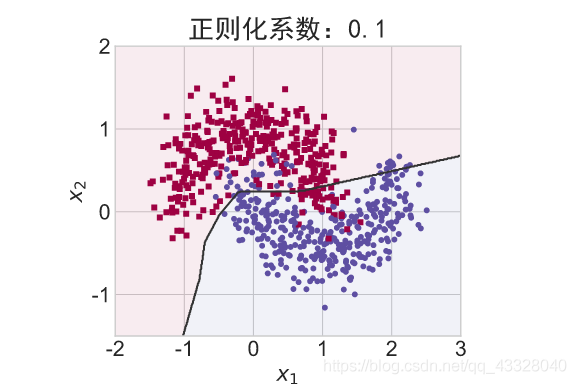
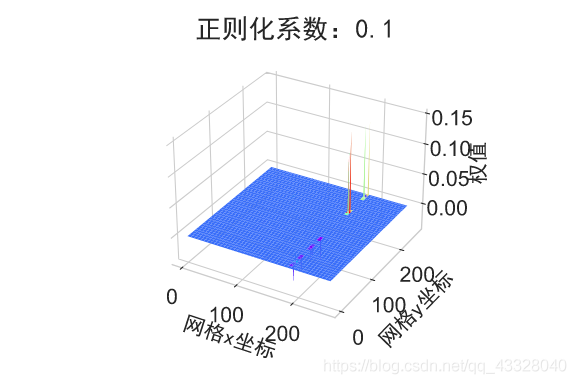
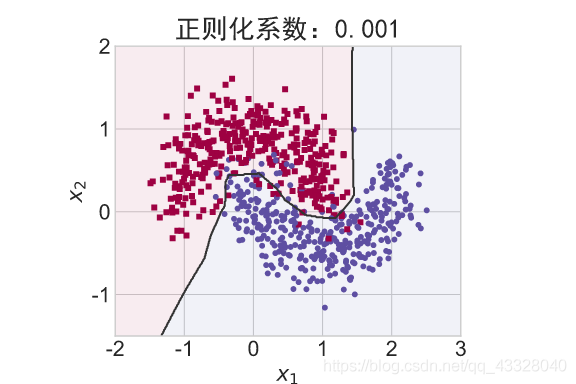
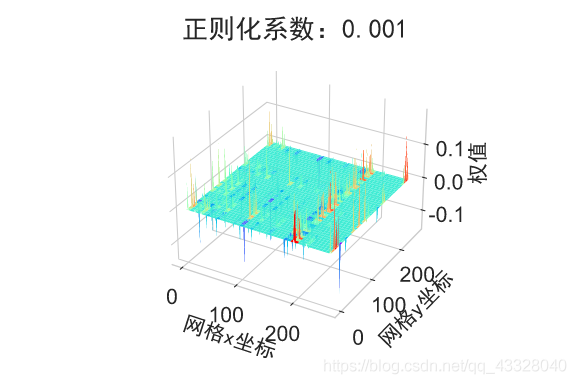
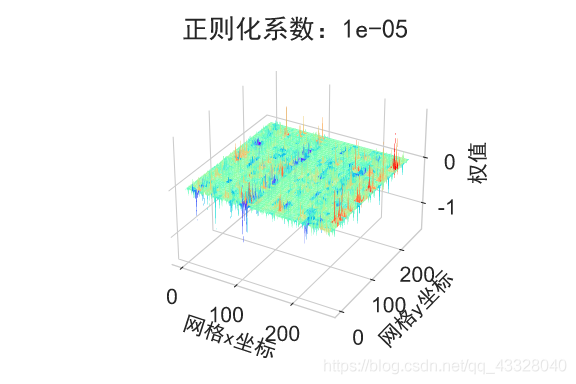
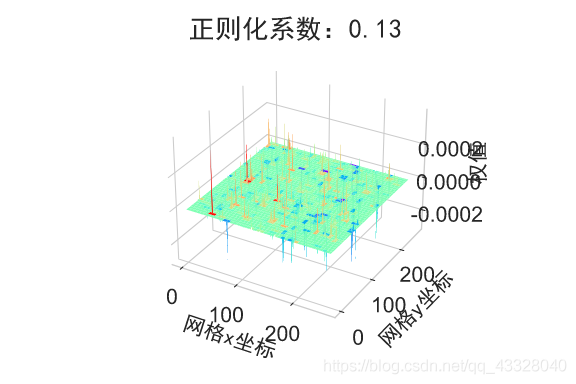
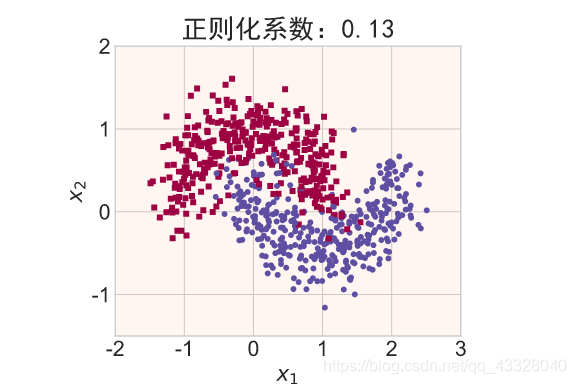
在保持网络结构不变的条件下,我们通过调节正则化系数 𝜆 = 0.00001,0.001,0.1,0.12,0.13 来测试网络的训练效果,并绘制出学习模型在训练集上的决策边界曲线
def regularizers_influence(X_train, y_train):
for _lambda in [1e-5, 1e-3, 1e-1, 0.12, 0.13]: # 设置不同的正则化系数
# 创建带正则化项的模型
model = build_model_with_regularization(_lambda)
# 模型训练
model.fit(X_train, y_train, epochs=N_EPOCHS, verbose=1)
# 绘制权值范围
layer_index = 2
plot_title = "正则化系数:{}".format(_lambda)
file_name = "正则化网络权值_" + str(_lambda)
# 绘制网络权值范围图
plot_weights_matrix(model, layer_index, plot_title, file_name, output_dir=OUTPUT_DIR + '/regularizers')
# 绘制不同正则化系数的决策边界线
# 可视化的 x 坐标范围为[-2, 3]
xx = np.arange(-2, 3, 0.01)
# 可视化的 y 坐标范围为[-1.5, 2]
yy = np.arange(-1.5, 2, 0.01)
# 生成 x-y 平面采样网格点,方便可视化
XX, YY = np.meshgrid(xx, yy)
preds = model.predict_classes(np.c_[XX.ravel(), YY.ravel()])
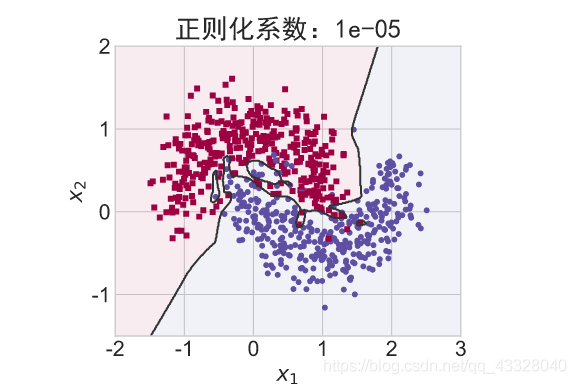
title = "正则化系数:{}".format(_lambda)
file = "正则化_%g.svg" % _lambda
make_plot(X_train, y_train, title, file, XX, YY, preds, output_dir=OUTPUT_DIR + '/regularizers')
regularizers_influence(X_train, y_train)
到此这篇关于详解tensorflow之过拟合问题实战的文章就介绍到这了,更多相关tensorflow 过拟合内容请搜索自学编程网以前的文章或继续浏览下面的相关文章希望大家以后多多支持自学编程网!

- 本文固定链接: https://zxbcw.cn/post/198720/
- 转载请注明:必须在正文中标注并保留原文链接
- QQ群: PHP高手阵营官方总群(344148542)
- QQ群: Yii2.0开发(304864863)
