浅谈SciPy中的optimize.minimize实现受限优化问题

问题描述：有一批样本x，每个样本都有几个固定的标签，如（男，24岁，上海），需要从中抽取一批样本，使样本总的标签比例满足分布P(x)，如（男:女=49%:51%、20岁:30岁=9%:11%、..........）

采用KL-散度作为优化目标函数。

KL-散度又叫相对熵

KL-散度在机器学习中，P用来表示样本的真实分布，比如[1,0,0]表示当前样本属于第一类。Q用来表示模型所预测的分布，比如[0.7,0.2,0.1]

KL-散度直观的理解就是如果用P来描述样本，那么就非常完美。而用Q来描述样本，虽然可以大致描述，但是不是那么的完美，信息量不足，需要额外的一些“信息增量”才能达到和P一样完美的描述。如果我们的Q通过反复训练，也能完美的描述样本，那么就不再需要额外的“信息增量”，Q等价于P。

公式：

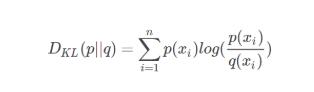
使用SciPy中的optimize.minimize来进行优化。

def minimize(fun, x0, args=(), method=None, jac=None, hess=None,
    hessp=None, bounds=None, constraints=(), tol=None,
    callback=None, options=None):

几个重要的参数：

fun:目标函数（he objective function to be minimized）；

x0:参数初始值（Initial guess. Array of real elements of size (n,)）；

bounds:参数取值范围限制（Bounds on variables for L-BFGS-B, TNC, SLSQP and trust-constr methods.）

constraints:约束函数（Constraints definition (only for COBYLA, SLSQP and trust-constr)

Constraints for COBYLA, SLSQP are defined as a list of dictionaries.
Each dictionary with fields:
 
 type : str
  Constraint type: 'eq' for equality, 'ineq' for inequality.
 fun : callable
  The function defining the constraint.
 jac : callable, optional
  The Jacobian of `fun` (only for SLSQP).
 args : sequence, optional
  Extra arguments to be passed to the function and Jacobian.
）

tol : 目标函数误差范围，控制迭代结束（optional Tolerance for termination. For detailed control, use solver-specific options.） options : 其他一些可选参数（dict, optional A dictionary of solver options. All methods accept the following generic options:）

求解过程：

定义优化函数：

def obj_function(x): 其中x为要优化的变量，在本问题中有480类的样本（如：男，24岁，上海），每类样本10-1000个不等，x为每类抽取的比例。要从中抽取50000个样本，满足22个约束条件（男:女=50%:50%、20岁:30岁=9%:11%等等）。

例如：男性要占总样本的50%，则

选择优化函数。SciPy中可以使用bounds参数的算法有：L-BFGS-B, TNC, SLSQP and trust-constr，可以使用constraints 参数的算法有： COBYLA, SLSQP and trust-constr

调参：optimize.minimize有统一的参数，但每个优化算法都有自己特有的参数，可以看源码中的参数列表。

运行：res = optimize.minimize(sample_fun, np.array(x0), bounds=bound, method='L-BFGS-B', tol=1e-11, options={'disp': True, 'maxiter': 300, 'maxfun': 1500000})，最终的结果保存在res.x中

如果程序没达到指定的迭代次数就停止，可能有两种原因：

STOP: TOTAL NO. of f AND g EVALUATIONS EXCEEDS LIMIT 增大参数maxfun；

CONVERGENCE: REL_REDUCTION_OF_F_<=_FACTR*EPSMCH 调小参数tol

以上这篇浅谈SciPy中的optimize.minimize实现受限优化问题就是小编分享给大家的全部内容了，希望能给大家一个参考，也希望大家多多支持自学编程网。