TensorFlow tf.nn.conv2d_transpose是怎样实现反卷积的

今天来介绍一下Tensorflow里面的反卷积操作，网上反卷积的用法的介绍比较少，希望这篇教程可以帮助到各位

反卷积出自这篇论文：Deconvolutional Networks，有兴趣的同学自行了解

首先无论你如何理解反卷积，请时刻记住一点，反卷积操作是卷积的反向

如果你随时都记住上面强调的重点，那你基本就理解一大半了，接下来通过一些函数的介绍为大家强化这个观念

conv2d_transpose(value, filter, output_shape, strides, padding="SAME", data_format="NHWC", name=None)

除去name参数用以指定该操作的name，与方法有关的一共六个参数：
第一个参数value：指需要做反卷积的输入图像，它要求是一个Tensor
第二个参数filter：卷积核，它要求是一个Tensor，具有[filter_height, filter_width, out_channels, in_channels]这样的shape，具体含义是[卷积核的高度，卷积核的宽度，卷积核个数，图像通道数]
第三个参数output_shape：反卷积操作输出的shape，细心的同学会发现卷积操作是没有这个参数的，那这个参数在这里有什么用呢？下面会解释这个问题
第四个参数strides：反卷积时在图像每一维的步长，这是一个一维的向量，长度4
第五个参数padding：string类型的量，只能是"SAME","VALID"其中之一，这个值决定了不同的卷积方式
第六个参数data_format：string类型的量，'NHWC'和'NCHW'其中之一，这是tensorflow新版本中新加的参数，它说明了value参数的数据格式。'NHWC'指tensorflow标准的数据格式[batch, height, width, in_channels]，'NCHW'指Theano的数据格式,[batch, in_channels，height, width]，当然默认值是'NHWC'

开始之前务必了解卷积的过程，参考我的另一篇文章：https://www.jb51.net/article/177798.htm

首先定义一个单通道图和3个卷积核

x1 = tf.constant(1.0, shape=[1,3,3,1])
kernel = tf.constant(1.0, shape=[3,3,3,1])

先别着急！我们不直接用反卷积函数，而是再定义一些图

x2 = tf.constant(1.0, shape=[1,6,6,3])
x3 = tf.constant(1.0, shape=[1,5,5,3])

x2是6×6的3通道图，x3是5×5的3通道图
好了，接下来对x3做一次卷积操作

y2 = tf.nn.conv2d(x3, kernel, strides=[1,2,2,1], padding="SAME")

所以返回的y2是一个单通道的图，如果你了解卷积过程，很容易看出来y2是[1，3，3，1]的Tensor，y2的结果如下：

[[[[ 12.]
  [ 18.]
  [ 12.]]
 
 [[ 18.]
  [ 27.]
  [ 18.]]
 
 [[ 12.]
  [ 18.]
  [ 12.]]]]

又一个很重要的部分！tf.nn.conv2d中的filter参数，是[filter_height, filter_width, in_channels, out_channels]的形式，而tf.nn.conv2d_transpose中的filter参数，是[filter_height, filter_width, out_channels，in_channels]的形式，注意in_channels和out_channels反过来了！因为两者互为反向，所以输入输出要调换位置

既然y2是卷积操作的返回值，那我们当然可以对它做反卷积，反卷积操作返回的Tensor，应该和x3的shape是一样的（不难理解，因为是卷积的反过程）

y3 = tf.nn.conv2d_transpose(y2,kernel,output_shape=[1,5,5,3], strides=[1,2,2,1],padding="SAME")

好，现在返回的y3果然是[1，5，5，3]的Tensor，结果如下：

[[[[ 12. 12. 12.]
  [ 30. 30. 30.]
  [ 18. 18. 18.]
  [ 30. 30. 30.]
  [ 12. 12. 12.]]
 
 [[ 30. 30. 30.]
  [ 75. 75. 75.]
  [ 45. 45. 45.]
  [ 75. 75. 75.]
  [ 30. 30. 30.]]
 
 [[ 18. 18. 18.]
  [ 45. 45. 45.]
  [ 27. 27. 27.]
  [ 45. 45. 45.]
  [ 18. 18. 18.]]
 
 [[ 30. 30. 30.]
  [ 75. 75. 75.]
  [ 45. 45. 45.]
  [ 75. 75. 75.]
  [ 30. 30. 30.]]
 
 [[ 12. 12. 12.]
  [ 30. 30. 30.]
  [ 18. 18. 18.]
  [ 30. 30. 30.]
  [ 12. 12. 12.]]]]

这个结果是怎么得来的？可以用一张动图来说明,图片来源：反卷积的真正含义

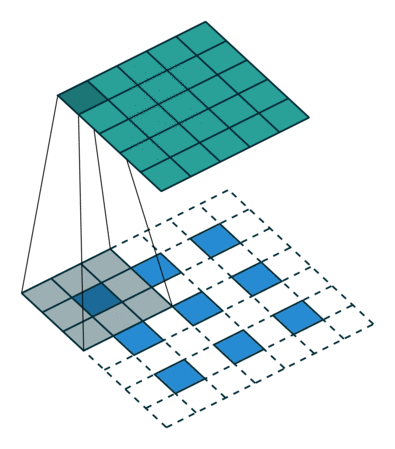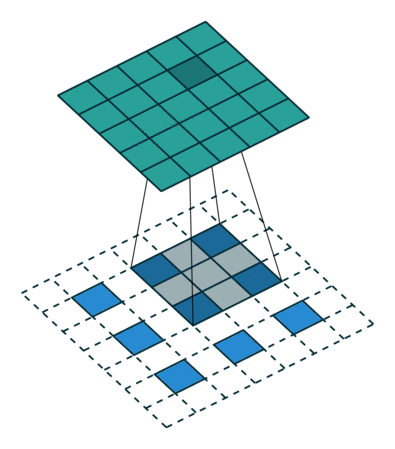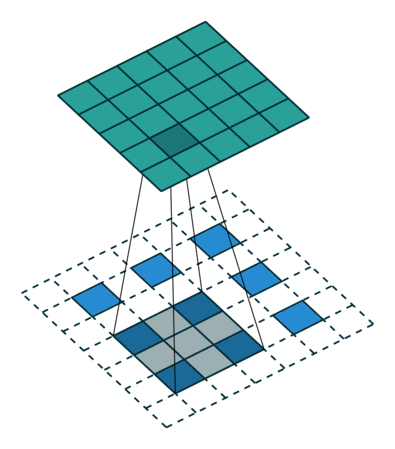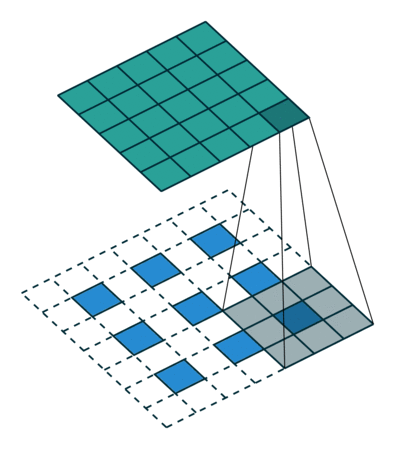
看起来，tf.nn.conv2d_transpose的output_shape似乎是多余的，因为知道了原图，卷积核，步长显然是可以推出输出图像大小的，那为什么要指定output_shape呢？
看这样一种情况：

y4 = tf.nn.conv2d(x2, kernel, strides=[1,2,2,1], padding="SAME")

我们把上面的x2也做卷积，获得shape为[1，3，3，1]的y4如下：

[[[[ 27.]
  [ 27.]
  [ 18.]]
 
 [[ 27.]
  [ 27.]
  [ 18.]]
 
 [[ 18.]
  [ 18.]
  [ 12.]]]]

[1，6，6，3]和[1，5，5，3]的图经过卷积得到了相同的大小，[1，3，3，1]
让我们再反过来看，那么[1，3，3，1]的图反卷积后得到什么呢？产生了两种情况。所以这里指定output_shape是有意义的，当然随意指定output_shape是不允许的，如下情况程序会报错：

y5 = tf.nn.conv2d_transpose(x1,kernel,output_shape=[1,10,10,3],strides=[1,2,2,1],padding="SAME")

以上是stride为2的情况，为1时也类似，当卷积核大于原图时，默认用VALID方式（用SAME就无意义了）参考下图：

程序清单：

import tensorflow as tf
 
x1 = tf.constant(1.0, shape=[1,3,3,1])
 
x2 = tf.constant(1.0, shape=[1,6,6,3])
 
x3 = tf.constant(1.0, shape=[1,5,5,3])
 
kernel = tf.constant(1.0, shape=[3,3,3,1])
 
 
 
y1 = tf.nn.conv2d_transpose(x1,kernel,output_shape=[1,6,6,3],
  strides=[1,2,2,1],padding="SAME")
 
y2 = tf.nn.conv2d(x3, kernel, strides=[1,2,2,1], padding="SAME")
 
y3 = tf.nn.conv2d_transpose(y2,kernel,output_shape=[1,5,5,3],
  strides=[1,2,2,1],padding="SAME")
 
y4 = tf.nn.conv2d(x2, kernel, strides=[1,2,2,1], padding="SAME")
 
'''
Wrong!!This is impossible
y5 = tf.nn.conv2d_transpose(x1,kernel,output_shape=[1,10,10,3],strides=[1,2,2,1],padding="SAME")
'''
sess = tf.Session()
tf.global_variables_initializer().run(session=sess)
x1_decov, x3_cov, y2_decov, x2_cov=sess.run([y1,y2,y3,y4])
print(x1_decov.shape)
print(x3_cov.shape)
print(y2_decov.shape)
print(x2_cov.shape)

到此这篇关于TensorFlow tf.nn.conv2d_transpose是怎样实现反卷积的的文章就介绍到这了,更多相关TensorFlow tf.nn.conv2d_transpose 反卷积内容请搜索自学编程网以前的文章或继续浏览下面的相关文章希望大家以后多多支持自学编程网！

编程技巧