本文实例为大家分享了C语言实现页面置换算法的具体代码,供大家参考,具体内容如下
操作系统实验
页面置换算法(FIFO、LRU、OPT)
概念:
1.最佳置换算法(OPT)(理想置换算法):从主存中移出永远不再需要的页面;如无这样的页面存在,则选择最长时间不需要访问的页面。于所选择的被淘汰页面将是以后永不使用的,或者是在最长时间内不再被访问的页面,这样可以保证获得最低的缺页率。
2.先进先出置换算法(FIFO):是最简单的页面置换算法。这种算法的基本思想是:当需要淘汰一个页面时,总是选择驻留主存时间最长的页面进行淘汰,即先进入主存的页面先淘汰。其理由是:最早调入主存的页面不再被使用的可能性最大。
3.最近最久未使用(LRU)算法:这种算法的基本思想是:利用局部性原理,根据一个作业在执行过程中过去的页面访问历史来推测未来的行为。它认为过去一段时间里不曾被访问过的页面,在最近的将来可能也不会再被访问。所以,这种算法的实质是:当需要淘汰一个页面时,总是选择在最近一段时间内最久不用的页面予以淘汰。
题目:
编写一个程序,实现本章所述的FIFO、LRU和最优页面置换算法。首先,生成一个随机的页面引用串,其中页码范围为0-9.将这个随机页面引用串应用到每个算法,并记录每个算法引起的缺页错误的数量。实现置换算法,一遍页面帧的数量可以从1~7。
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
int numbers[20]={7,0,1,2,
0,3,0,4,
2,3,0,3,
2,1,2,0,
1,7,0,1};//本地数据,与课本一致,方便测试
int nums=0;//输入栈的个数,为了方便使用,
int stack[20][7]={10};
void begin();
void randomnum();//用于产生随机数
void init();//初始化
void FIFO();//FIFO算法
void LRU();//LRU算法
void OPT();//最优页面置换算法(OPT)
void print();//输出
int main() {
begin();
FIFO();
LRU();
OPT();
return 0;
}
void begin()//开始菜单界面
{
int i,j,k;
printf("请输入页面帧的数量(1-7):");
scanf("%d",&nums);
for(k=0;;k++)
{
printf("是否使用随机数产生输入串(0:是,1:否)");
scanf("%d",&j);
if(j==0)
{
randomnum();
break;
}
else if(j==1)
{
break;
}
else
{
printf("请输入正确的选择!\n");
}
}
printf("页面引用串为:\n");
for(i=0;i<20;i++)
{
printf("%d ",numbers[i]);
}
printf("\n");
init();
}
void randomnum()//如果需要使用随机数生成输入串,调用该函数
{
srand(time(0));//设置时间种子
for(int i = 0; i < 20; i++) {
numbers[i] = rand() % 10;//生成区间0`9的随机页面引用串
}
}
void init()//用于每次初始化页面栈中内容,同时方便下面输出的处理
{
int i,j;
for(i=0;i<20;i++)
for(j=0;j<nums;j++)
stack[i][j]=10;
}
void print()//输出各个算法的栈的内容
{
int i,j;
for(i=0;i<nums;i++)
{
for(j=0;j<20;j++)
{
if(stack[j][i]==10)
printf("* ");
else
printf("%d ",stack[j][i]);
}
printf("\n");
}
}
void FIFO()//FIFO算法
{
init();
int i,j=1,n=20,k,f,m;
stack[0][0]=numbers[0];
for(i=1;i<20;i++)
{
f=0;
for(m=0;m<nums;m++)
{
stack[i][m]=stack[i-1][m];
}
for(k=0;k<nums;k++)
{
if(stack[i][k]==numbers[i])
{
n--;
f=1;
break;
}
}
if(f==0)
{
stack[i][j]=numbers[i];
j++;
}
if(j==nums)
j=0;
}
printf("\n");
printf("FIFO算法:\n");
print();
printf("缺页错误数目为:%d\n",n);
}
void LRU()//LRU算法
{
int i,j,m,k,sum=1;
int sequence[7]={0};//记录序列
init();
stack[0][0]=numbers[0];
sequence[0]=nums-1;
for(i=1;i<nums;i++)//前半部分,页面空置的情况
{
for(j=0;j<nums;j++)
{
stack[i][j]=stack[i-1][j];
}
for(j=0;j<nums;j++)
{
if(sequence[j]==0)
{
stack[i][j]=numbers[i];
break;
}
}
for(j=0;j<i;j++)//将之前的优先级序列都减1
{
sequence[j]--;
}
sequence[i]=nums-1;//最近使用的优先级列为最高
sum++;
}
for(i=nums;i<20;i++)//页面不空,需要替换的情况
{
int f;
f=0;
for(j=0;j<nums;j++)
{
stack[i][j]=stack[i-1][j];
}
for(j=0;j<nums;j++)//判断输入串中的数字,是否已经在栈中
{
if(stack[i][j]==numbers[i])
{
f=1;
k=j;
break;
}
}
if(f==0)//如果页面栈中没有,不相同
{
for(j=0;j<nums;j++)//找优先序列中为0的
{
if(sequence[j]==0)
{
m=j;
break;
}
}
for(j=0;j<nums;j++)
{
sequence[j]--;
}
sequence[m]=nums-1;
stack[i][m]=numbers[i];
sum++;
}
else//如果页面栈中有,替换优先级
{
if(sequence[k]==0)//优先级为最小优先序列的
{
for(j=0;j<nums;j++)
{
sequence[j]--;
}
sequence[k]=nums-1;
}
else if(sequence[k]==nums-1)//优先级为最大优先序列的
{
//无需操作
}
else//优先级为中间优先序列的
{
for(j=0;j<nums;j++)
{
if(sequence[k]<sequence[j])
{
sequence[j]--;
}
}
sequence[k]=nums-1;
}
}
}
printf("\n");
printf("LRU算法:\n");
print();
printf("缺页错误数目为:%d\n",sum);
}
void OPT()//OPT算法
{
int i,j,k,sum=1,f,q,max;
int seq[7]={0};//记录序列
init();
stack[0][0]=numbers[0];
seq[0]=nums-1;
for(i=1;i<nums;i++)//前半部分,页面空置的情况
{
for(j=0;j<nums;j++)
{
stack[i][j]=stack[i-1][j];
}
for(j=0;j<nums;j++)
{
if(seq[j]==0)
{
stack[i][j]=numbers[i];
break;
}
}
for(j=0;j<i;j++)//将之前的优先级序列都减1
{
seq[j]--;
}
seq[i]=nums-1;//最近使用的优先级列为最高
sum++;
}
for(i=nums;i<20;i++)//后半部分,页面栈中没有空的时候情况
{
//k=nums-1;//最近的数字的优先级
for(j=0;j<nums;j++)//前面的页面中内容赋值到新的新的页面中
{
stack[i][j]=stack[i-1][j];
}
for(j=0;j<nums;j++)
{
f=0;
if(stack[i][j]==numbers[i])
{
f=1;
break;
}
}
if(f==0)//页面中没有,需要替换的情况
{
for(q=0;q<nums;q++)//优先级序列中最大的就是最久未用的,有可能出现后面没有在用过的情况
{
seq[q]=20;
}
for(j=0;j<nums;j++)//寻找新的优先级
{
for(q=i+1;q<20;q++)
{
if(stack[i][j]==numbers[q])
{
seq[j]=q-i;
break;
}
}
}
max=seq[0];
k=0;
for(q=0;q<nums;q++)
{
if(seq[q]>max)
{
max=seq[q];
k=q;
}
}
stack[i][k]=numbers[i];
sum++;
}
else
{
//页面栈中有需要插入的数字,无需变化,替换的优先级也不需要变化
}
}
printf("\n");
printf("OPT算法:\n");
print();
printf("缺页错误数目为:%d\n",sum);
}
运行结果截图:
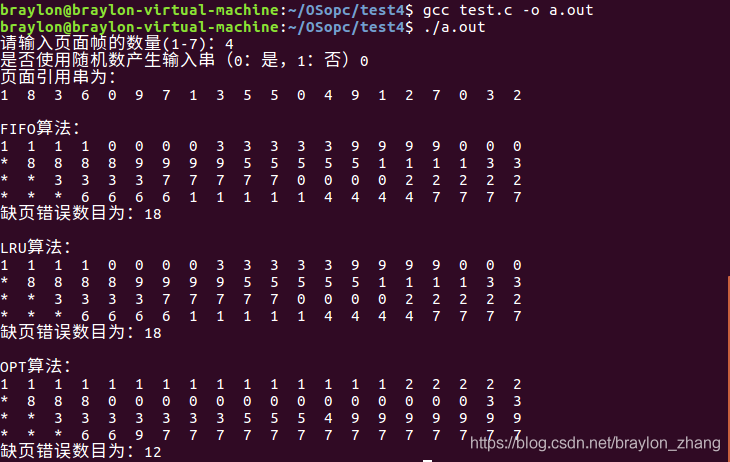


这个代码能在linux上跑通的,在windows上肯定也没得问题
以上就是本文的全部内容,希望对大家的学习有所帮助,也希望大家多多支持自学编程网。

- 本文固定链接: https://zxbcw.cn/post/203092/
- 转载请注明:必须在正文中标注并保留原文链接
- QQ群: PHP高手阵营官方总群(344148542)
- QQ群: Yii2.0开发(304864863)
