聊聊Python中的浮点数运算不准确问题

大家好，老 Amy 来了。之前就意识到一个问题，但是最近又有朋友提出来了，所以就想着干脆记录下来，分享给大家叭~

啥问题呢？请看题：

也就是说，需要大家计算1.1-1的值，很多朋友会说：“emmm…这还不简单，玩我呢？不就是0.1嘛”

但是如果你用 python 去执行一下，会发现结果跟你想的不太一样，如下图：

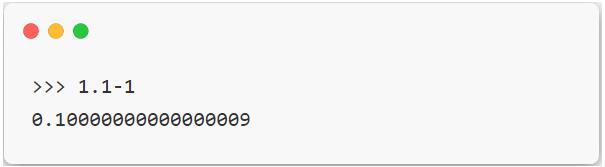
这样大家是不是发现了什么问题？是的，浮点数在运算过程中并没有保证完全精确，是什么原因导致了这种现象呢？很多朋友就会窃喜：“这不就是 Python 的 bug 嘛~”

但实际上，这并不是 Python 中的 bug ，它和计算机硬件中如何处理浮点数有关。浮点数在计算机硬件中以二进制的形式存在，但是我们现在看到的都是十进制，而十进制的浮点数不能都完全精确的表示为二进制小数。

就比如说我们在十进制数中无法用小数精确表示 1/3 一样，在二进制数中也无法用小数精确表示 1/10。显然这样子的说明并没有十进制中的 1/3 那么直观，接下来我们尝试去计算一下二进制中的 1/10 :

十进制的整数位是二进制的整数位，十进制的小数位是二进制数的小数位。那现在我们拿到0.1

整数部分为0

小数部分为0.1，并顺序取值

0.1*2=0.2<1取0
0.2*2=0.4<1取0
0.4*2=0.8<1取0
0.8*2=1.6>1取1
0.6*2=1.2>1取1
0.2*2=0.4<1取0
…

有没有发现？在二进制下，1/10 是一个无限循环小数：0.00011001100110011…，显然这样的表示形式无法精确的表示浮点数，最终的结果是近似 1/10 。在使用 IEEE-754 浮点运算标准的计算机硬件上，Python 的浮点数映射为 IEEE-754 双精度浮点数，共包含 53 位精度（这里指的是二进制），在这个范围下，这个最接近 1/10 的结果是：

3602879701896397/2∗∗55

这表示在计算机硬件中，1/10 的真实十进制数值为：

0.1000000000000000055511151231257827021181583404541015625

那如何进行精确的浮点数运算呢？有朋友提出四舍五入可以解决。那我们来仔细看一下四舍五入真的可以解决这个问题吗？

四舍五入进行解决

在 python 中，使用 round(number[, ndigits]) 来进行四舍五入，其中 ndigits 表示保留几位小数，默认为0。

我们来看代码如下：

In [10]: round(0.6)
Out[10]: 1
In [11]: round(0.65,1)
Out[11]: 0.7
In [12]: round(0.64,1)
Out[12]: 0.6

上面代码符合我们四舍五入的预期结果，但是不要着急，我们接着往下看：

In [13]: round(1.15,1)
Out[13]: 1.1
In [14]: round(0.5)
Out[14]: 0
In [15]: round(1.5)
Out[15]: 2

这样看是不是有些问题，什么问题呢？按照四舍五入的话，round(1.15)会直接进为1.2，但是此时并没有，而是变为了1.1。这是为什么呢？

如果没有上面对浮点数的了解，仅从表象上很难去解释。我们已经知道了在计算机内部，对于一些浮点数是无法精确表示的，比如上面代码中 1.15，我们可以通过 format() 来看看它在计算机内部更加具体的数值：

In [16]: format(1.15,".51f")
Out[16]: '1.149999999999999911182158029987476766109466552734375'

看到这个结果，我们就恍然大悟，为什么看到的结果会是1.1了。

但是接下来，可能会更加的困惑，因为对于 0.5 来说，是完全可以直接转为二进制表示的。但是round(0.5)结果却为0？这是因为 round() 的工作原理为：对于 round(number[, ndigits])，如果 number 可以被正常处理，则它的值会被舍入到最接近的 10 的负 ndigits 次幂的倍数上，对于与两个倍数的差值（差值的绝对值）均相等的情况，则会选择两个倍数中的偶数。

# 最接近的10的负0次幂的倍数为0、1，并与0、1差值的绝对值相同，选择偶数0
>>> round(0.5) 
0
# 最接近的10的负2次幂的倍数为0.12、0.13，并与0.12、0.13的差值的绝对值相同，选择偶数0.12
>>> round(0.125, 2) 
0.12
# 最接近的10的负2次幂的倍数为0.13
>>> round(0.12548828125, 2) 
0.13

这个规则，用我们熟悉的话来说即为“ 四舍六入五成双 ”。

使用decimal进行浮点数的精确计算

那我们在 Python 中怎么进行精确的浮点数计算呢，Python 标准库为我们提供了decimal 这个模块来解决这个问题，decimal 常用于需要精确处理浮点数的场合，比如银行账户金额、货币加减等。

In [17]: from decimal import Decimal
In [18]: 0.1-0.09
Out[18]: 0.010000000000000009
In [19]: Decimal('0.1')-Decimal('0.09')
Out[19]: Decimal('0.01')

同样，我们可以使用它来查看对于不能精确表示的浮点数在计算机内部的具体数值：

In [20]: Decimal.from_float(1.1)
Out[20]: Decimal('1.100000000000000088817841970012523233890533447265625')
In [21]: Decimal.from_float(0.1)
Out[21]: Decimal('0.1000000000000000055511151231257827021181583404541015625')

这样就可以解决我们的困惑与问题啦~

补充：python做浮点数运算时的坑记录

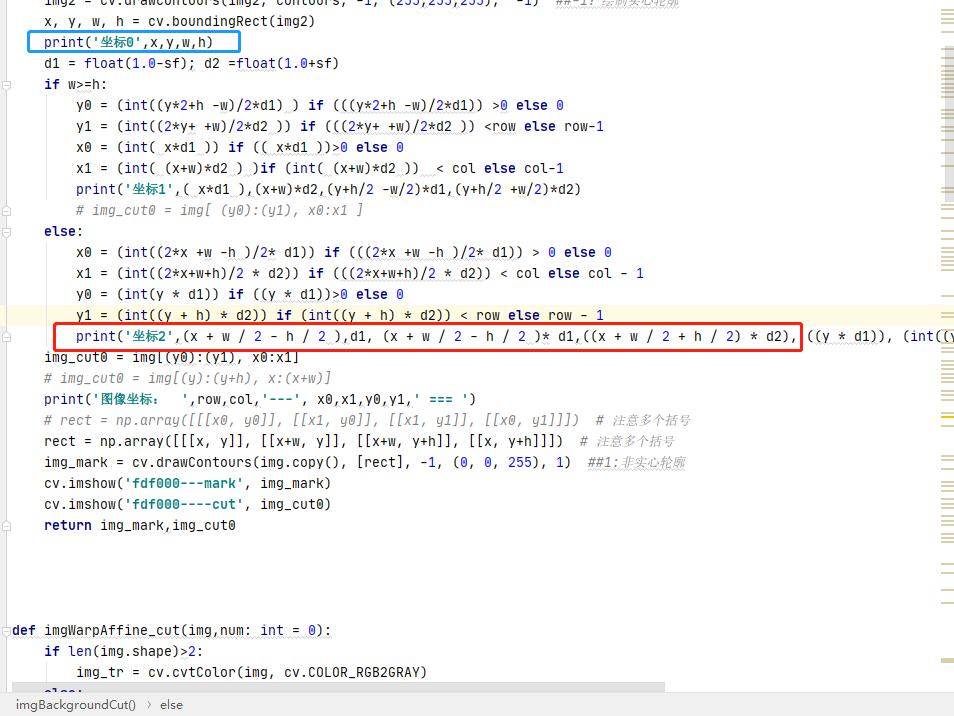
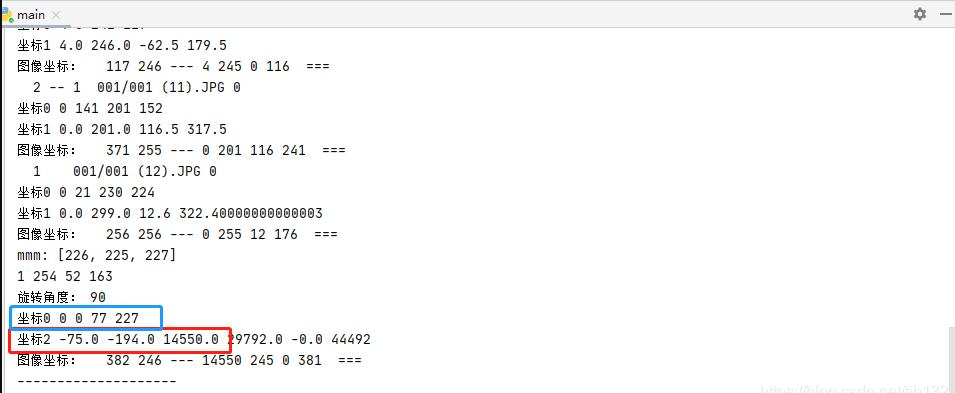
很显然，这个计算结果是不对的，而且偏离实际值十分远。。。。。。。。

太坑人了这。

本来想自动截取计算得到的图片尺寸，但是这计算结果，坑害了半天的查找错误过程！！！！

以上为个人经验，希望能给大家一个参考，也希望大家多多支持自学编程网。如有错误或未考虑完全的地方，望不吝赐教。