1.Training: 如何训练模型
一句话理解机器学习一般训练过程 :通过有标签样本来调整(学习)并确定所有权重Weights和偏差Bias的理想值。
训练的目标:最小化损失函数
(损失函数下面马上会介绍)
机器学习算法在训练过程中,做的就是:检查多个样本并尝试找出可最大限度地减少损失的模型;目标就是将损失(Loss)最小化
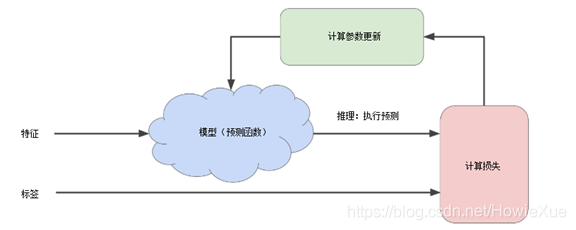
上图就是一般模型训练的一般过程(试错过程),其中
- 模型: 将一个或多个特征作为输入,然后返回一个预测 (y') 作为输出。为了进行简化,不妨考虑一种采用一个特征并返回一个预测的模型,如下公式(其中b为 bias,w为weight)
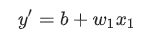
- 计算损失:通过损失函数,计算该次参数(bias、weight)下的loss。
- 计算参数更新:检测损失函数的值,并为参数如bias、weight生成新值,以降低损失为最小。
例如:使用梯度下降法,因为通过计算整个数据集中w每个可能值的损失函数来找到收敛点这种方法效率太低。所以通过梯度能找到损失更小的方向,并迭代。
举个TensorFlow代码栗子,对应上面公式在代码中定义该线性模型:
y_output = tf.multiply(w,x) + b
假设该模型应用于房价预测,那么y_output为预测的房价,x为输入的房子特征值(如房子位置、面积、楼层等)
2. Loss Function:损失和损失函数
损失是一个数值 表示对于单个样本而言模型预测的准确程度。
如果模型的预测完全准确,则损失为零,否则损失会较大。
训练模型的目标是从所有样本中找到一组平均损失“较小”的权重和偏差。
损失函数的目标:准确找到预测值和真实值的差距
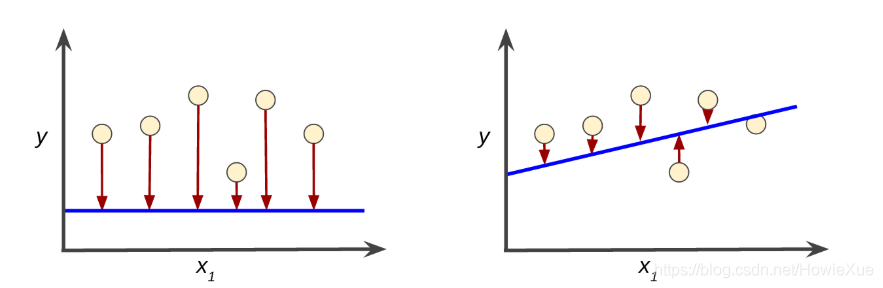
如图 红色箭头表示损失,蓝线表示预测。明显左侧模型的损失较大;右侧模型的损失较小
要确定loss,模型必须定义损失函数 loss function。例如,线性回归模型通常将均方误差用作损失函数,而逻辑回归模型则使用对数损失函数。
正确的损失函数,可以起到让预测值一直逼近真实值的效果,当预测值和真实值相等时,loss值最小。
举个TensorFlow代码栗子,在代码中定义一个损失loss_price 表示房价预测时的loss,使用最小二乘法作为损失函数:
loss_price = tr.reduce_sum(tf.pow(y_real - y_output), 2)
这里,y_real是代表真实值,y_output代表模型输出值(既上文公式的y' ),因为有的时候这俩差值会是负数,所以会对误差开平方,具体可以搜索下最小二乘法公式
3. Gradient Descent:梯度下降法
理解梯度下降就好比在山顶以最快速度下山:
好比道士下山,如何在一座山顶上,找到最短的路径下山,并且确定最短路径的方向
原理上就是凸形问题求最优解,因为只有一个最低点;即只存在一个斜率正好为 0 的位置。这个最小值就是损失函数收敛之处。
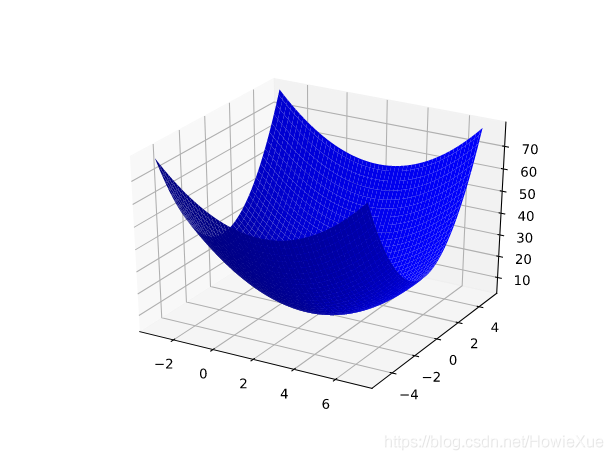
通过计算整个数据集中 每个可能值的损失函数来找到收敛点这种方法效率太低。我们来研究一种更好的机制,这种机制在机器学习领域非常热门,称为梯度下降法。
梯度下降法的目标:寻找梯度下降最快的那个方向
梯度下降法的第一个阶段是为 选择一个起始值(起点)。起点并不重要;因此很多算法就直接将 设为 0 或随机选择一个值。下图显示的是我们选择了一个稍大于 0 的起点:
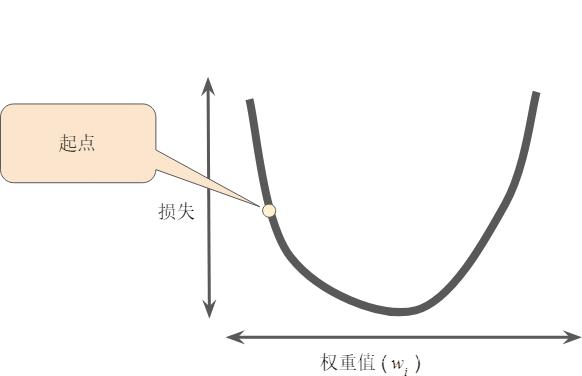
然后,梯度下降法算法会计算损失曲线在起点处的梯度。简而言之,梯度是偏导数的矢量;它可以让您了解哪个方向距离目标“更近”或“更远”。请注意,损失相对于单个权重的梯度(如图 所示)就等于导数。
请注意,梯度是一个矢量,因此具有以下两个特征:
- 方向
- 大小
梯度始终指向损失函数中增长最为迅猛的方向。梯度下降法算法会沿着负梯度的方向走一步,以便尽快降低损失
为了确定损失函数曲线上的下一个点,梯度下降法算法会将梯度大小的一部分与起点相加
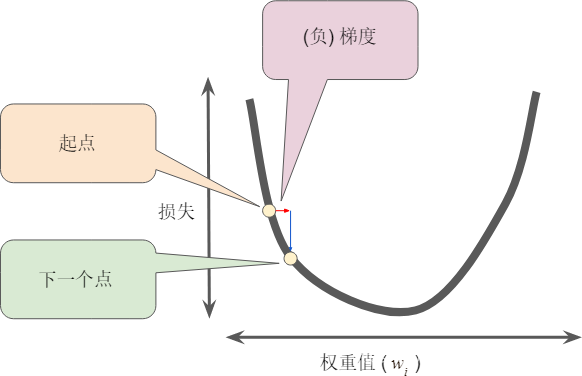
然后,梯度下降法会重复此过程,逐渐接近最低点。(找到了方向)
- 随机梯度下降法SGD:解决数据过大,既一个Batch过大问题,每次迭代只是用一个样本(Batch为1),随机表示各个batch的一个样本都是随机选择。
4. Learning Rate:学习速率
好比上面下山问题中,每次下山的步长。
因为梯度矢量具有方向和大小,梯度下降法算法用梯度乘以一个称为学习速率(有时也称为步长)的标量,以确定下一个点的位置。这是超参数,用来调整AI算法速率
例如,如果梯度大小为 2.5,学习速率为 0.01,则梯度下降法算法会选择距离前一个点 0.025 的位置作为下一个点。
超参数是编程人员在机器学习算法中用于调整的旋钮。大多数机器学习编程人员会花费相当多的时间来调整学习速率。如果您选择的学习速率过小,就会花费太长的学习时间:
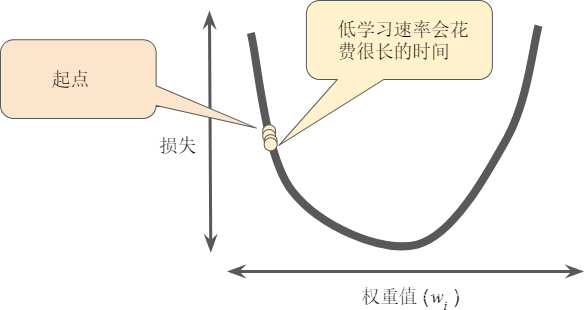
继续上面的栗子,实现梯度下降代码为:
train_step = tf.train.GradientDescentOptimizer(0.025).minimize(loss_price)
这里设置梯度下降学习率为0.025, GradientDescentOptimizer()就是使用的随机梯度下降算法, 而loss_price是由上面的损失函数获得的loss
至此有了模型、损失函数以及梯度下降函数,就可以进行模型训练阶段了:
Session = tf.Session()
Session.run(init)
for _ in range(1000):
Session.run(train_step, feed_dict={x:x_data, y:y_data})
这里可以通过for设置固定的training 次数,也可以设置条件为损失函数的值低于设定值,
x_data y_data则为训练所用真实数据,x y 是输入输出的placeholder(代码详情参见TensorFlow API文档)
5. 扩展:BP神经网络训练过程
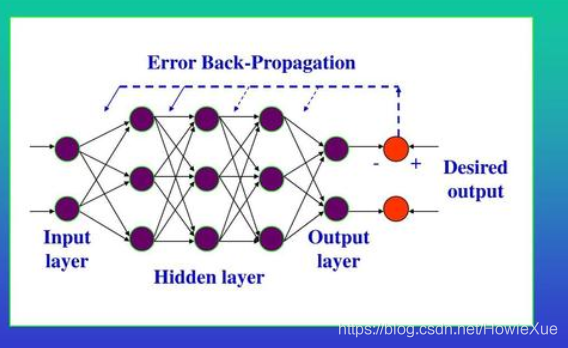
BP(BackPropagation)网络的训练,是反向传播算法的过程,是由数据信息的正向传播和误差Error的反向传播两个过程组成。
反向传播算法是神经网络算法的核心,其数学原理是:链式求导法则
- 正向传播过程:
输入层通过接收输入数据,传递给中间层(各隐藏层)神经元,每一个神经元进行数据处理变换,然后通过最后一个隐藏层传递到输出层对外输出。
- 反向传播过程:
正向传播后通过真实值和输出值得到误差Error,当Error大于设定值,既实际输出与期望输出差别过大时,进入误差反向传播阶段:
Error通过输出层,按照误差梯度下降的方式,如上面提到的随机梯度下降法SGD,反向修正各层参数(如Weights),向隐藏层、输入层逐层反转。
通过不断的正向、反向传播,直到输出的误差减少到预定值,或到达最大训练次数。
到此这篇关于AI:如何训练机器学习的模型的文章就介绍到这了,相信对你有所帮助,更多相关机器学习内容请搜索自学编程网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持自学编程网!

- 本文固定链接: https://zxbcw.cn/post/209757/
- 转载请注明:必须在正文中标注并保留原文链接
- QQ群: PHP高手阵营官方总群(344148542)
- QQ群: Yii2.0开发(304864863)
