Python机器学习之逻辑回归

一、题目

1.主题：逻辑回归

2.描述：假设你是某大学招生主管，你想根据两次考试的结果决定每个申请者的录取
机会。现有以往申请者的历史数据，可以此作为训练集建立逻辑回归模型，并用
其预测某学生能否被大学录取。

3.数据集：文件 ex2data1.txt ，第一列、第二列分别表示申请者两次
考试的成绩，第三列表示录取结果（1 表示录取，0 表示不录取）。

二、目的

1.理解逻辑回归模型

2.掌握逻辑回归模型的参数估计算法

三、平台

1.硬件：计算机

2.操作系统：WINDOWS

3.编程软件：Pycharm

4.开发语言：python

四、基本原理

注：基本原理是我们在学习逻辑回归过程中的一些总结，包括为什么要选择对数损失函数等。

4.1 逻辑回归

逻辑回归就是将样本的特征可样本发生的概率联合起来，概率就是一个数，所以就是解决分类问题，一般解决二分类问题。
对于线性回归中，f ( x ) = w T x + b ，这里 f ( x ) 的范围为[ − ∞ , + ∞ ]，说明通过线性回归中我们可以求得任意的一个值。对于逻辑回归来说就是概率，这个概率取值需要在区间[0,1]内，通常我们使用Sigmoid函数表示。

Sigmoid函数其表达式为（2）

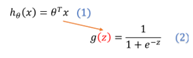
最终我们可以通过Sigmoid函数求出对于每组自变量使得因变量预测为1的概率P；

即：

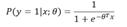
（当P>0.5时预测为1，小于0.5为0）
在分类情况下，经过学习后的LR分类器其实就是一组权值θ ，当有测试样本输入时，这组权值与测试数据按照加权得到

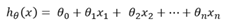
之后按照Sigmoid函数的形式求出

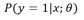
从而去判断每个测试样本所属的类别。

4.2 损失函数

实验一我们做线性回归模型时，给出了线性回归的代价函数的形式（误差平方和函数），具体形式如：

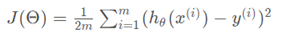
但是并不能应用到逻辑回归中，这是因为LR的假设函数的外层函数是Sigmoid函数，Sigmoid函数是一个复杂的非线性函数，这就使得我们将逻辑回归的假设函数

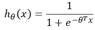
带入上式时，我们得到的 是一个非凸函数，如下图：

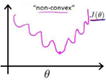
因此，此处我们需要重新考虑损失函数；
在逻辑回归中，我们最常用的损失函数为对数损失函数，对数损失函数可以为LR提供一个凸的代价函数，有利于使用梯度下降对参数求解。对数函数图像如图：

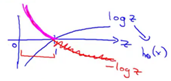
蓝色的曲线表示的是对数函数的图像，红色的曲线表示的是负对数 的图像，该图像在0-1区间上有一个很好的性质，如图粉红色曲线部分。在0-1区间上当z=1时，函数值为0，而z=0时，函数值为无穷大。这就可以和代价函数联系起来，在预测分类中当算法预测正确其代价函数应该为0；当预测错误，我们就应该用一个很大代价（无穷大）来惩罚我们的学习算法，使其不要轻易预测错误。
因此，我们重新定义逻辑回归的代价函数为：

损失函数的求解为：

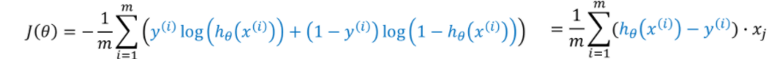
五、实验步骤

1.数据可视化

在python中通过文件导入数据，并使用matlibplot工具建立对应散点图：

需要注意的是，我们的theta是三元组，θ0对应的X特征值固定为1，因此读取数据时，如上图最左侧加入一个1；

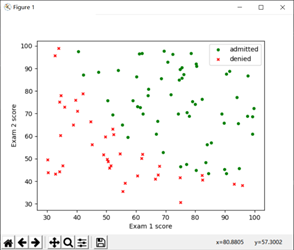
可以看到，被录取与不被录取的数据有较为清晰的一个界限，接下来我们要求解的就是这条界线；

2. 将线性回归参数初始化为0，计算代价函数(cost function)的初始值

根据基本原理中的代价计算公式，这里将sigmoid、损失公式代码化：

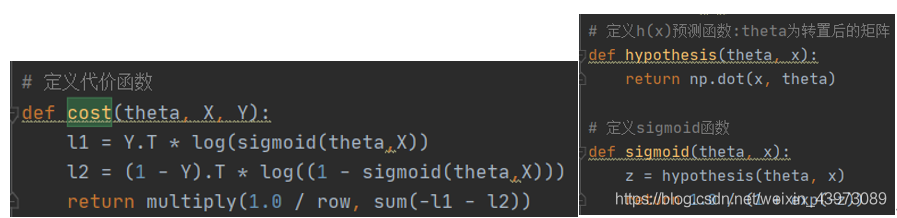
将theta初始化为（0，0，0）后，直接调用cost函数求值：

得到代价函数初始值：

3. 选择一种优化方法求解逻辑回归参数

(1)梯度下降法

我们选择先用梯度下降法来观察theta参数结果；
梯度下降算法代码实现如图：

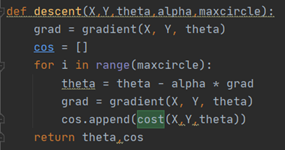
X：对于线性回归中的常量b，我们可以将它的系数视为1，然后和变量x组成一个m行3列的矩阵，其中m是数据规模，这个矩阵就是X。
Y：一个m行1列的矩阵，对应是否录取。
alpha：学习率
第一步，将我们的Θ初始化为[[0][0][0]]。
第二步，对于给定的步长alpha和此时的梯度gradient，更新我们的theta。然后计算此时thrta对应的梯度更新gradient。
第三步，重复第二步30万次
第四步，返回theta，即为我们线性回归的参数。

但是，对于逻辑回归来说，这里遇到了一个问题，那就是alpha和迭代次数的取值，如果alpha过小，损失函数将收敛的非常慢，迭代次数达到40万时才勉强收敛，但如果alpha过大，又会导致过大的步长使得准确率下降；
alpha = 0.001时的收敛函数，在50万次时收敛： 0.005时在25万次时收敛；

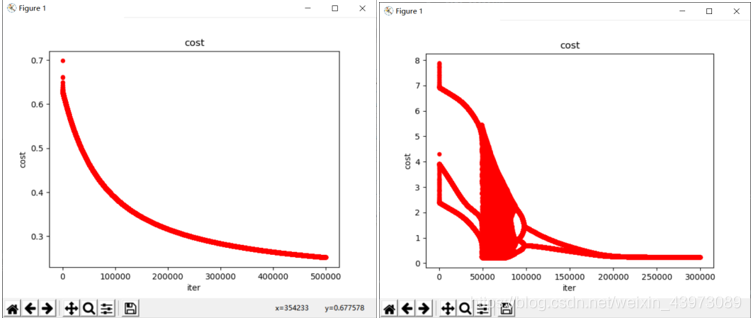
而如果alpha继续增大（如0.01），将导致不够准确，其界限与收敛图形如下：

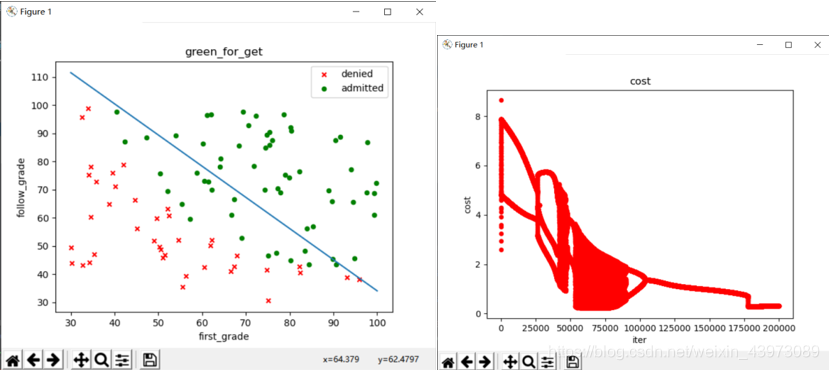
（界限太差，仅80%准确率，且需要20万次迭代）
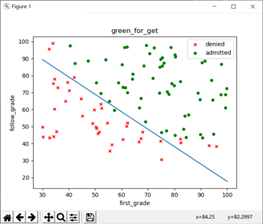
因此，我们在运行该数据时需要运行稍长的时间；alpha=0.005，迭代次数为30万时可以得到一组回归参数：

它的划分边界如图所示，其准确率为92%：该参数的划分准确率计算方法如下：

测试准确率：

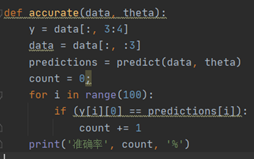
比较简单，预测正确则加一，最后除以全部样本数。

(2)牛顿迭代法

因为上述的迭代下降法所需迭代次数过多，因此这里使用一种优化方法来求解参数；

方法介绍

牛顿迭代法的原理较为复杂，因此不在这里写出来。
对比这牛顿迭代法方法与梯度下降法的参数更新公式可以发现，两种方法不同在于牛顿法中多了一项二阶导数，这项二阶导数对参数更新的影响主要体现在 改变参数更新方向上。

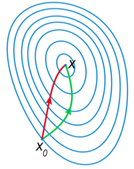
如图所示，红色是牛顿法参数更新的方向，绿色为梯度下降法参数更新方向，因为牛顿法考虑了二阶导数，因而可以找到更优的参数更新方向，在每次更新的步幅相同的情况下，可以比梯度下降法节省很多的迭代次数。
迭代过程：

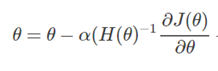
代码实现

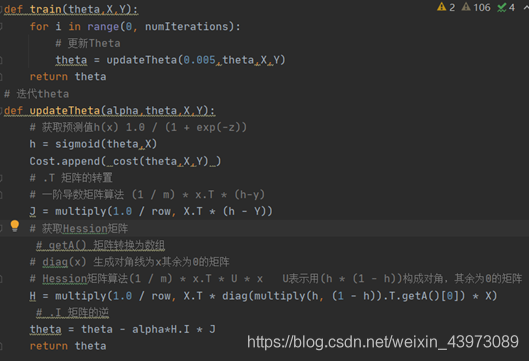
h值为sigmoid函数求得的概率；
J为一阶偏导数
H为Hession矩阵（海森矩阵），二阶偏导数

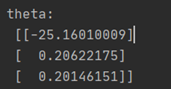
牛顿迭代法得到的theta：

优点

对于同样的学习率alpha = 0.005，cost仅需要1000次迭代就差不多收敛了；
而如果放大alpha，如alpha = 0.5，那么它只需要迭代10次即可收敛。

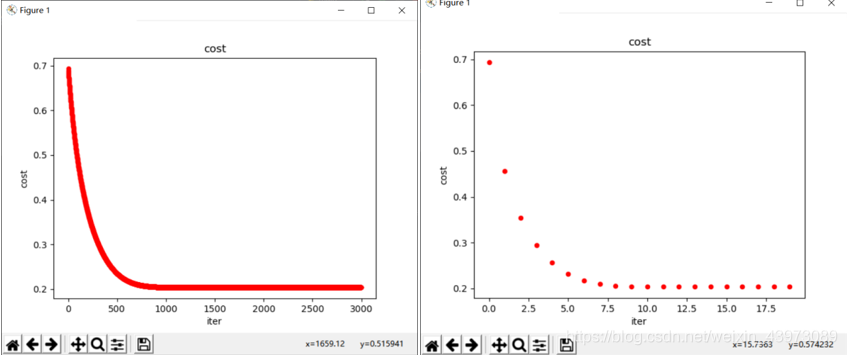
并且准确率保持在89%（数据较小）；

3. 某学生两次考试成绩分别为 42、85，预测其被录取的概率

这里直接使用sigmoid函数以及牛顿迭代法求得的theta来进行其概率的计算：

得到结果：

即，y=1的概率为0.65145509，也就是被录取的概率

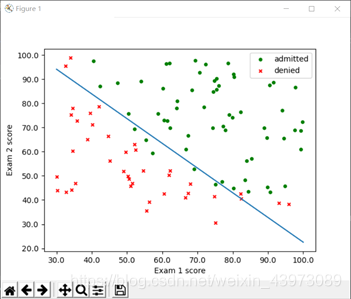
4. 画出分类边界

在上面已经画出了梯度下降法的分类边界，这里给出牛顿迭代法的边界

到此这篇关于Python机器学习之逻辑回归的文章就介绍到这了,更多相关Python逻辑回归内容请搜索自学编程网以前的文章或继续浏览下面的相关文章希望大家以后多多支持自学编程网！