树的同构
举例
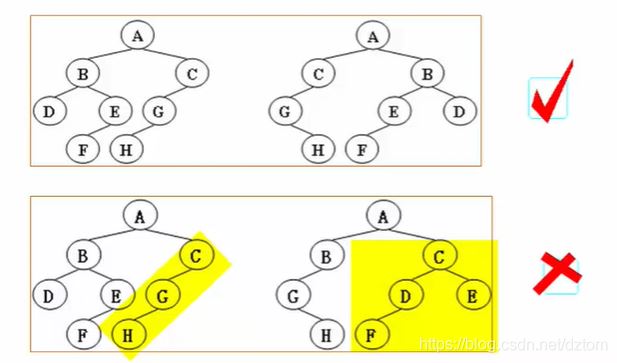
树的构造
树可以由数组或链表来构造:
举例:上图左上角的树通过数组可表示为
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | D | E | G | - | - | - | F | - | H | - |
该方式浪费了部分空间,但适合表示完全二叉树
链表方式则比较直观
除上述两种方式外,还可以采用“类数组”的方式
public static class Node{
String data;
int left;
int right;
}
举例:上图左上角的树可表示为
| 数组索引 | data | left | right |
|---|---|---|---|
| 0 | A | 1 | 2 |
| 1 | B | 3 | 4 |
| 2 | C | 6 | - |
| 3 | D | - | - |
| 4 | E | 5 | - |
| 5 | F | - | - |
| 6 | G | 7 | - |
| 7 | H | - | - |
本文的树结构使用了第三种方式
终端输入:
A,1,2 B,3,- C,-,- D,-,- A,2,1 B,3,- C,-,- D,-,-
public class TongGou {
private Scanner scanner;
public TongGou(){
scanner = new Scanner(System.in);
}
//树结构
public static class Node{
String data;
int left;
int right;
}
/**
* 创建树
* @param nodes
* @return
*/
public int createTree(Node[] nodes){
int N = nodes.length;
int root = -1;
int[] check = new int[N];
Arrays.fill(check,0); //初始化为0
for (int i=0;i<N;i++){
//输入格式 data,left,right
String next = scanner.next();
String[] inputList = next!=null?next.split(","):null;
if(inputList!=null&&inputList.length==3){
nodes[i] = new Node();
int left = "-".equals(inputList[1])?-1:Integer.parseInt(inputList[1]);
int right = "-".equals(inputList[2])?-1:Integer.parseInt(inputList[2]);
nodes[i].data = inputList[0];
nodes[i].left = left;
nodes[i].right = right;
if(left>0) {
check[left] = 1;
}
if(right>0){
check[right] = 1;
}
}
}
for(int i=0;i<check.length;i++){
if(check[i]==0&&nodes[i].data!=null){
root = i;
break;
}
}
return root;
}
/**
* 判断同构
* @param r1
* @param r2
* @return
*/
public boolean isomorphic(int r1,int r2,Node[] t1,Node[] t2){
//须注意不要漏掉逻辑!
//两个根节点均为null,必同构
if ((r1 == -1) && (r2 == -1)) {
return true;
}
//一个非空 另一个空,必不同构
if(((r1==-1)&&(r2!=-1))||((r1!=-1)&&(r2==-1))){
return false;
}
//两个节点非空 但值不同,必不同构
if(!t1[r1].data.equals(t2[r2].data)){
return false;
}
//两根节点的左孩子为空条件下,则须判断两根节点的右子树是否同构
if(t1[r1].left==-1&&t2[r2].left==-1){
return isomorphic(t1[r1].right,t2[r2].right,t1,t2);
}
//两根节点的左孩子不为空且左孩子的值也相同,须判断两根节点的左子树是否同构以及两根节点的右子树是否同构
//如果左右子树均同构,则整棵树同构
if((t1[r1].left!=-1&&t2[r2].left!=-1)&&(t1[t1[r1].left].data.equals(t2[t2[r2].left].data))){
return isomorphic(t1[r1].left,t2[r2].left,t1,t2)&&isomorphic(t1[r1].right,t2[r2].right,t1,t2);
}else{
//分两种情况解释:
//1、两根节点的左孩子不为空,但左孩子的值不同
//例如:t1[r1.left].data!=t2[r2.left].data。但有t1[r1.left].data==t2[r2.right].data、t1[r1.right].data==t2[r2.left].data
//即有可能r1的左子树与r2的右子树同构、r1的右子树与r2的左子树同构
//故须判断r1的左子树是否与r2的右子树同构,以及r1的右子树是否与r2的左子树同构
//2、两根节点的左孩子一个为空,一个不为空
//例如:r1.left==-1、r2.left!=-1,如果r2.right==-1,显然r1的左子树与r2的右子树同构,此时则有可能r1的右子树与r2的左子树同构
//故须判断r1的左子树是否与r2的右子树同构,以及r1的右子树是否与r2的左子树同构
return isomorphic(t1[r1].left,t2[r2].right,t1,t2)&&isomorphic(t1[r1].right,t2[r2].left,t1,t2);
}
}
public static void main(String[] args) {
TongGou tongGou = new TongGou();
Node[] nodes = new Node[4];
Node[] nodes1 = new Node[4];
int tree1 = tongGou.createTree(nodes);
System.out.println();
int tree2 = tongGou.createTree(nodes1);
boolean isomorphic = tongGou.isomorphic(tree1, tree2, nodes, nodes1);
System.out.println(isomorphic);
}
}
总结
本篇文章的内容就到这了,希望大家可以喜欢,也希望大家可以多多关注自学编程网的其他精彩内容!

- 本文固定链接: https://zxbcw.cn/post/215769/
- 转载请注明:必须在正文中标注并保留原文链接
- QQ群: PHP高手阵营官方总群(344148542)
- QQ群: Yii2.0开发(304864863)
