栈
栈的基本操作



InitStack(&S):初始化
StackEmpty(S):判空,空则true,非空则false
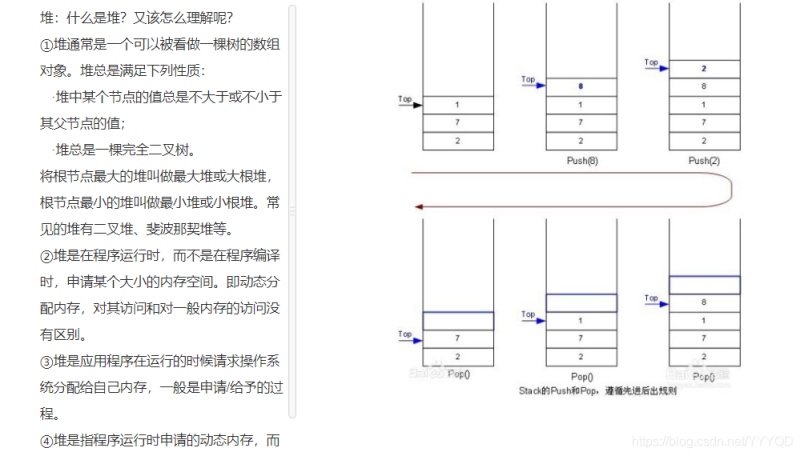
Push(&S,x):入栈
Pop(&S,&x):出栈,并用x返回元素内容
GetTop(S,&x):读栈顶元素
DestroyStack(&S):销毁并释放空间
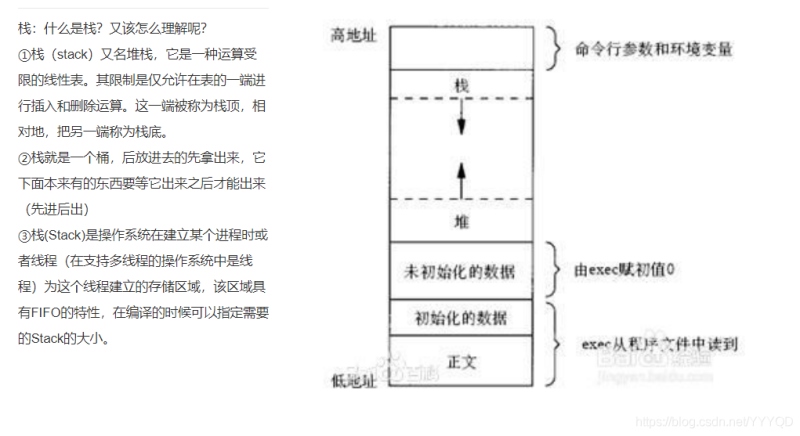
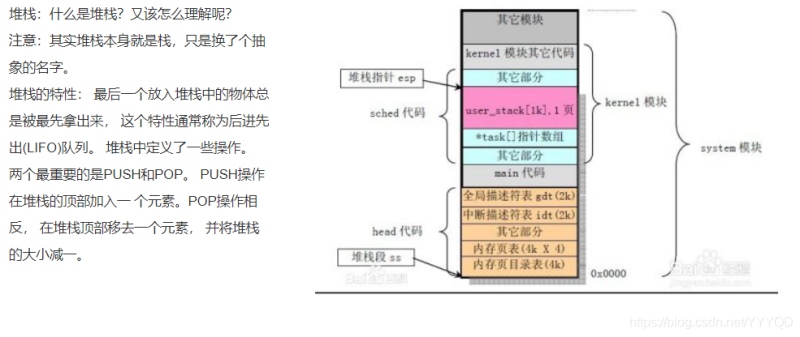
栈是一种受限的线性表,只允许在一端操作
栈若只能在栈顶操作,则只可能上溢
采用非递归方式重写递归时,不一定要用栈,比如菲波那切数列只要用循环即可
共享栈:
从两头往中间填充,有效的利用空间。
出栈序列的个数:1𝑛+1𝐶2𝑛𝑛
队列
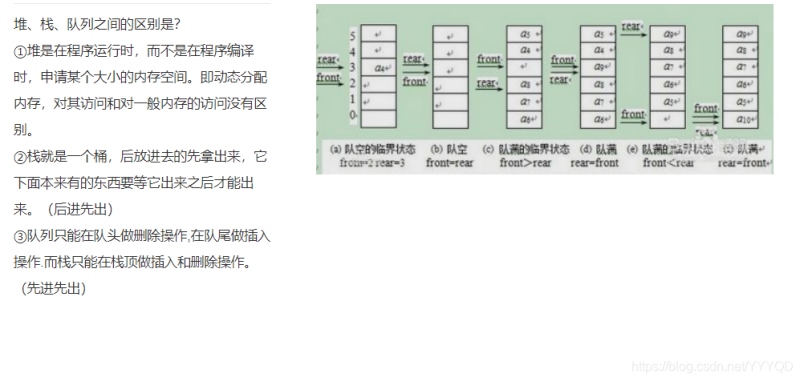
队列也是受限的线性表,只允许在一端插入,另一端删除
FIFO(First in first out)
常见操作:
InitQueue(&Q):初始化,构造一个空队列Q
QueueEmpty(Q):判空
EnQueue(&Q,x):入队
DeQueue(&Q,&x):出队并返回出队的元素至x
GetHead(Q,&x):获取对头元素
队列的大题真题考的是,画初始状态,判空判满的条件,入队基本过程
So先看类似的概念,想法,思路,后期再看具体的代码实现,毕竟没考过具体代码
顺序存储定义:
#define Maxsize 50
typedef struct{
Elemtype data[Maxsize];
int front,rear;
}SqQueue;
循环队列:
初始化:Q.front=Q.rear=0
队首指针+1\入队:Q.front=(Q.front+1)%Maxsize
队尾指针+1\出队:Q.rear=(Q.rear+1)%Maxsize
队列长度:(Q.rear+Maxsize-Q.front)%Maxsize
因为队满和队空都是Q.front=Q.rear,所以无法判断到底是队空还是队满
有三个解决办法
1)常用方法:牺牲一个单元来区分队空和队满,入队是少用一个单元
队满条件:(Q.rear+1)%MaxsizeQ.front
队空条件:Q.frontQ.rear
队列中元素个数:(Q.rear-Q.front+Maxsize)%Maxsize
2)类型中增设一个数据成员表示元素个数,这样队空:Q.size0,队满:Q.sizeMaxsize
3)增设tag,入队时令tag=1,出队时令tag=0,这样能表示当Q.frontQ.rear时,如果tag1,则队满,tag==0则队空
链式存储:
typedef struct LinkNode{ //定义节点
Elemtype data;
struct LinkNode *next;
}LinkNode;
typedef struct{ //定义队列的首尾节点
Node *front,*rear;
}LinkQueue;
栈和队列的应用
括号匹配
表达式求值
后缀表达式:数据进栈,操作符则弹出2个数据进行操作再将结果进栈
同一个问题,递归算法和非递归算法一般来说,非递归效率比较低,因为有很多重复计算
图的广度优先算法要借助辅助队列
将中缀表达式转换为前缀表达式
转换步骤如下:
初始化两个栈:运算符栈s1,储存中间结果的栈s2
从右至左扫描中缀表达式
遇到操作数时,将其压入s2
遇到运算符时,比较其与s1栈顶运算符的优先级
如果s1为空,或栈顶运算符为右括号“)”,则直接将此运算符入栈
否则,若优先级比栈顶运算符的较高或相等,也将运算符压入s1
否则,将s1栈顶的运算符弹出并压入到s2中,再次转到(4-1)与s1中新的栈顶运算符相比较
遇到括号时
如果是右括号“)”,则直接压入s1
如果是左括号“(”,则依次弹出S1栈顶的运算符,并压入S2,直到遇到右括号为止,此时将这一对括号丢弃
重复步骤2至5,直到表达式的最左边
将s1中剩余的运算符依次弹出并压入s2
依次弹出s2中的元素并输出,结果即为中缀表达式对应的前缀表达式
将中缀表达式转换为后缀表达式
与转换为前缀表达式相似,步骤如下:
初始化两个栈:运算符栈s1和储存中间结果的栈s2;
从左至右扫描中缀表达式;
遇到操作数时,将其压s2;
遇到运算符时,比较其与s1栈顶运算符的优先级:
如果s1为空,或栈顶运算符为左括号“(”,则直接将此运算符入栈;
否则,若优先级比栈顶运算符的高,也将运算符压入s1(注意转换为前缀表达式时是优先级较高或相同,而这里则不包括相同的情况);
否则,将s1栈顶的运算符弹出并压入到s2中,再次转到(4-1)与s1中新的栈顶运算符相比较;
遇到括号时:
如果是左括号“(”,则直接压入s1;
如果是右括号“)”,则依次弹出s1栈顶的运算符,并压入s2,直到遇到左括号为止,此时将这一对括号丢弃;
重复步骤2至5,直到表达式的最右边;
将s1中剩余的运算符依次弹出并压入s2;
依次弹出s2中的元素并输出,结果的逆序即为中缀表达式对应的后缀表达式(转换为前缀表达式时不用逆序)
特殊矩阵的压缩存储
对称矩阵
三角矩阵
三对角矩阵:又称带状矩阵
稀疏矩阵:三元组既可以用数组存储,也可以用十字链表法
总结
本篇文章就到这里了,希望能给你带来帮助,也希望您能够多多关注自学编程网的更多内容!

- 本文固定链接: https://www.zxbcw.cn/post/220936/
- 转载请注明:必须在正文中标注并保留原文链接
- QQ群: PHP高手阵营官方总群(344148542)
- QQ群: Yii2.0开发(304864863)
