首页 > 编程语言 > OpenCV半小时掌握基本操作之傅里叶变换
2022
10-31

OpenCV半小时掌握基本操作之傅里叶变换

概述

OpenCV 是一个跨平台的计算机视觉库, 支持多语言, 功能强大. 今天小白就带大家一起携手走进 OpenCV 的世界. 

在这里插入图片描述

高频 vs 低频

高频 vs 低频:

  • 高频: 变换剧烈的灰度分量, 例如边界
  • 低频: 变换缓慢的灰度分量, 例如一片大海

在这里插入图片描述

滤波:

  • 低通滤波器: 只保留低频, 会使得图像模糊
  • 高通滤波器: 只保留高频, 会使得图像细节增强

傅里叶变换

傅里叶变化 (Fourier Transform) 是一种分析信号的方法. 傅里叶变化可分析信号的成分, 也可以用这些成分合成信号.

效果:

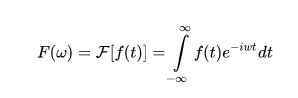
在这里插入图片描述

傅里叶变换:

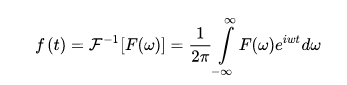
在这里插入图片描述

傅里叶逆变换:

在这里插入图片描述

在 OpenCV 中实现傅里叶变换的函数是cv2.dft()和cv2.idft()(傅里叶逆变化)

代码详解

输入转换

傅里叶变换支持的输入格式是np.float32, 所以我们需要先把图像转换到要求的格式.

代码实现:

import numpy as np
import cv2

# 读取图片, 并转换成灰度图
img = cv2.imread("Mona_Lisa.jpg", cv2.IMREAD_GRAYSCALE)
print(img.dtype)  # unit8数据类型

# 转换成np.float32
img_float32 = np.float32(img)
print(img_float32.dtype)  # float32数据类型

输出结果:

uint8
float32

傅里叶变换

格式:

cv2.dft(src, dst=None, flags=None, nonzeroRows=None)

参数:

  • src: 输入图像
  • dst: 输出图像, 默认为 None
  • flags: 转换标志 (5 种)
  • nonezeroRows: 要处理的 dst 行数, 默认为 None

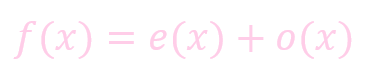
在这里插入图片描述

返回值:

  • 实部和虚部 (双通道)
  • 实部: 代表所有的偶函数 (余弦函数) 的部分
  • 虚部: 代表所有的奇函数 (正弦函数) 的部分

代码实现:

# 傅里叶变换
dft = cv2.dft(img_float32, flags=cv2.DFT_COMPLEX_OUTPUT)

# 中心转换, 将低频挪到中心
dft_shift = np.fft.fftshift(dft)

获取幅度谱

幅度谱 (Magnitude Spectrum), 即从构成波形的频率侧面看过去, 每一个频率分量都会在侧面的投影, 如图:

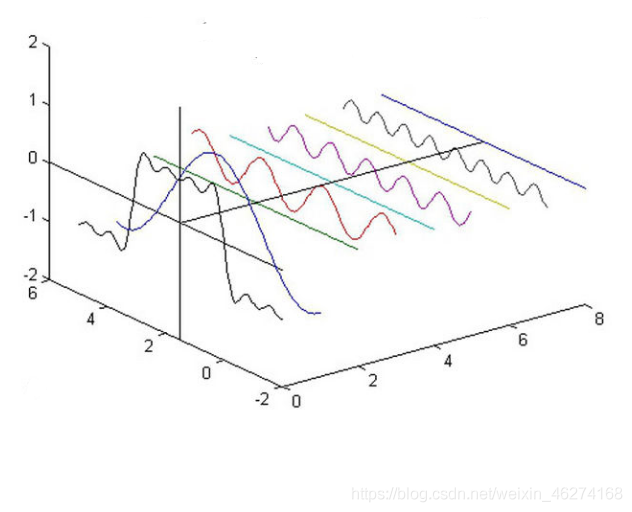
在这里插入图片描述

通过```cv2.magnitude``我们可以极端二维矢量的幅值.

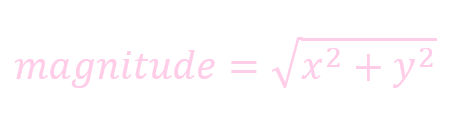
在这里插入图片描述

格式:

cv2.magnitude(x, y, magnitude=None)

参数:

  • x: 实部
  • y: 虚部

代码实现:

# 获取幅度谱, 映射到灰度空间 [0, 255]
magnitude_spectrum = 20 * np.log(cv2.magnitude(dft_shift[:, :, 0], dft_shift[:, :, 1]))

# 幅度谱展示
combine = np.hstack((img, magnitude_spectrum.astype(np.uint8)))
cv2.imshow("combine", combine)
cv2.waitKey(0)
cv2.destroyAllWindows()

输出结果:

在这里插入图片描述

傅里叶逆变换

格式:

cv2.idft(src, dst=None, flags=None, nonzeroRows=None)

参数:

  • src: 输入图像
  • dst: 输出图像, 默认为 None
  • flags: 转换标志 (5 种)
  • nonezeroRows: 要处理的 dst 行数, 默认为 None

返回值:

  • 实部和虚部 (双通道)
  • 实部: 代表所有的偶函数 (余弦函数) 的部分
  • 虚部: 代表所有的奇函数 (正弦函数) 的部分

代码实现:

# 获取中心位置
rows, cols = img.shape
crow, ccol = int(rows / 2), int(cols / 2)

# 低通滤波
mask = np.zeros((rows, cols, 2), np.uint8)
mask[crow - 30:crow + 30, ccol - 30:ccol + 30] = 1

# 傅里叶逆变换
fshidt = dft_shift * mask
f_ishift = np.fft.ifftshift(fshidt)
img_back = cv2.idft(f_ishift)

获取低频

import numpy as np
import cv2

# 读取图片, 并转换成灰度图
img = cv2.imread("Mona_Lisa.jpg", cv2.IMREAD_GRAYSCALE)
print(img.dtype)  # unit8数据类型

# 转换成np.float32
img_float32 = np.float32(img)
print(img_float32.dtype)  # float32数据类型

# 傅里叶变换
dft = cv2.dft(img_float32, flags=cv2.DFT_COMPLEX_OUTPUT)

# 中心转换, 将低频挪到中心
dft_shift = np.fft.fftshift(dft)

# 获取幅度谱
magnitude_spectrum = 20 * np.log(cv2.magnitude(dft_shift[:, :, 0], dft_shift[:, :, 1]))

# 幅度谱展示
combine = np.hstack((img, magnitude_spectrum.astype(np.uint8)))
cv2.imshow("combine", combine)
cv2.waitKey(0)
cv2.destroyAllWindows()

# 获取中心位置
rows, cols = img.shape
crow, ccol = int(rows / 2), int(cols / 2)

# 低通滤波
mask = np.zeros((rows, cols, 2), np.uint8)
mask[crow - 30:crow + 30, ccol - 30:ccol + 30] = 1
fshidt = dft_shift * mask
f_ishift = np.fft.ifftshift(fshidt)

# 傅里叶逆变换, 获取低频图像
img_back = cv2.idft(f_ishift)
img_back = cv2.magnitude(img_back[:, :, 0], img_back[:, :, 1])

# 结果展示
img_back = 255 * cv2.normalize(img_back, None, norm_type=cv2.NORM_MINMAX, dtype=cv2.CV_32F)  # 标准化
result = np.hstack((img, img_back.astype(np.uint8)))
cv2.imshow("result", result)
cv2.waitKey(0)
cv2.destroyAllWindows()

输出结果:

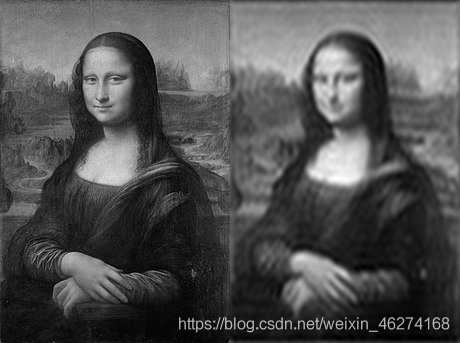
在这里插入图片描述

在这里插入图片描述

获取高频

import numpy as np
import cv2

# 读取图片, 并转换成灰度图
img = cv2.imread("Mona_Lisa.jpg", cv2.IMREAD_GRAYSCALE)
print(img.dtype)  # unit8数据类型

# 转换成np.float32
img_float32 = np.float32(img)
print(img_float32.dtype)  # float32数据类型

# 傅里叶变换
dft = cv2.dft(img_float32, flags=cv2.DFT_COMPLEX_OUTPUT)

# 中心转换, 将低频挪到中心
dft_shift = np.fft.fftshift(dft)

# 获取幅度谱
magnitude_spectrum = 20 * np.log(cv2.magnitude(dft_shift[:, :, 0], dft_shift[:, :, 1]))

# 幅度谱展示
combine = np.hstack((img, magnitude_spectrum.astype(np.uint8)))
cv2.imshow("combine", combine)
cv2.waitKey(0)
cv2.destroyAllWindows()

# 获取中心位置
rows, cols = img.shape
crow, ccol = int(rows / 2), int(cols / 2)

# 高通滤波
mask = np.ones((rows, cols, 2), np.uint8)
mask[crow - 30:crow + 30, ccol - 30:ccol + 30] = 0
fshidt = dft_shift * mask
f_ishift = np.fft.ifftshift(fshidt)

# 傅里叶逆变换, 获取高频图像
img_back = cv2.idft(f_ishift)
img_back = cv2.magnitude(img_back[:, :, 0], img_back[:, :, 1])

# 结果展示
img_back = 255 * cv2.normalize(img_back, None, norm_type=cv2.NORM_MINMAX, dtype=cv2.CV_32F)  # 标准化
result = np.hstack((img, img_back.astype(np.uint8)))
cv2.imshow("result", result)
cv2.waitKey(0)
cv2.destroyAllWindows()

输出结果:

在这里插入图片描述

在这里插入图片描述

到此这篇关于OpenCV半小时掌握基本操作之傅里叶变换的文章就介绍到这了,更多相关OpenCV傅里叶变换内容请搜索自学编程网以前的文章或继续浏览下面的相关文章希望大家以后多多支持自学编程网！

编程技巧