分类：曲线

2021
10-12

python一绘制元二次方程曲线的实例分析

说明1、Matplotlib函数可以绘制图形，使用plot函数绘制曲线。2、需要将200个点的x坐标和Y坐标分别以序列的形式输入plot函数，然后调用show函数来显示图形。实例importmatplotlib.pyplotasplt#200个点的x坐标x=range(-100,100)#生成y点的坐标y=[i**2foriinx]#绘制一元二次曲线plt.plot(x,y)#调用savefig将一元二次曲线保存为result.jpgplt.savefig('result.jpg')#如果直接写成plt.savefig('cos')会生成cos.pngplt.show()... 继续阅读 >

2021
03-07

pytorch绘制曲线的方法

本文实例为大家分享了pytorch绘制曲线的具体代码，供大家参考，具体内容如下importtorchimporttorch.nn.functionalasFfromtorch.autogradimportVariableimportmatplotlib.pyplotasplt#fakedatax=torch.linspace(-5,5,200)#xdata(tensor),shape=(100,1)x=Variable(x)#创建variable（变量），构造神经网络要使用Variable类型x_np=x.data.numpy()#numpyarrayforplotting，用于绘图的numpy数组#fo... 继续阅读 >

2021
02-21

python绘制高斯曲线

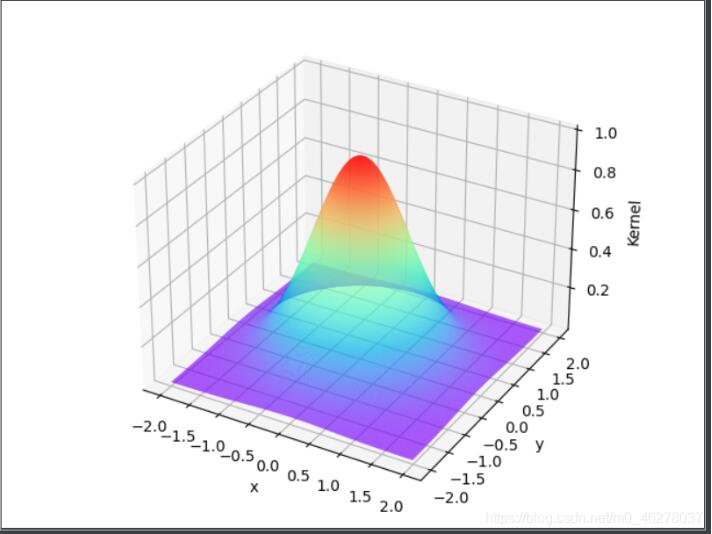本文实例为大家分享了python绘制高斯曲线的具体代码，供大家参考，具体内容如下源码：importnumpyasnpimportmatplotlib.pyplotaspltimportmathimportmpl_toolkits.mplot3dimporttensorflow.compat.v1astftf.disable_v2_behavior()#importtensorflowastffromsklearnimportdatasetssess=tf.InteractiveSession()gamma=tf.constant(-1.0)x,y=np.mgrid[-2:2:0.01,-2:2:0.01]x_data=tf.placeholder(shape=[4... 继续阅读 >

2020
10-08

基于python实现ROC曲线绘制广场解析

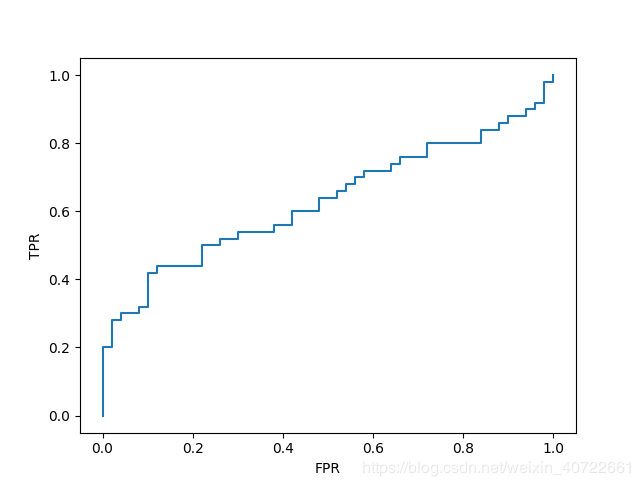ROC结果源数据:鸢尾花数据集（仅采用其中的两种类别的花进行训练和检测）Summaryfeatures：['sepallength(cm)','sepalwidth(cm)','petallength(cm)','petalwidth(cm)']实例：[5.1,3.5,1.4,0.2]target：'setosa''versicolor'（0,1）采用回归方法进行拟合得到参数和biasmodel.fit(data_train,data_train_label)对测试数据进行预测得到概率值res=model.predict(data[:100])与训练集labels匹配后进行排序（从大到... 继续阅读 >

2020
09-27

python matplotlib模块基本图形绘制方法小结【直线，曲线，直方图，饼图等】

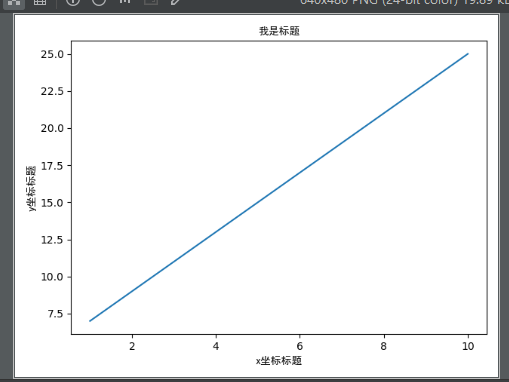本文实例讲述了pythonmatplotlib模块基本图形绘制方法。分享给大家供大家参考，具体如下：matplotlib模块是python中一个强大的绘图模块安装pip install matplotlib首先我们来画一个简单的图来感受它的神奇importnumpyasnpimportmatplotlib.pyplotaspltimportmatplotlibzhfont1=matplotlib.font_manager.FontProperties(fname="SimHei.ttf")#-------设置字体，这个可以事先下载https://www.fontpalace.com/fon... 继续阅读 >

2020
09-27

使用OpenGL绘制Bezier曲线

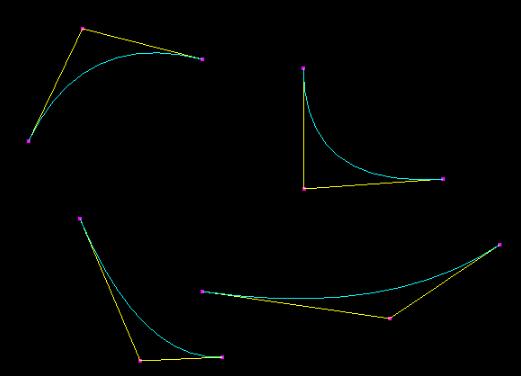本文实例为大家分享了OpenGL绘制Bezier曲线的具体代码，供大家参考，具体内容如下最近在看FrancisSHill,Jr和StephenMKelley合著的《计算机图形学》(OpenGL版)(第三版)书中有绘制三个控制点的Bezier曲线的代码。自己重新敲了一遍代码。发现了其中的一点小错误，修正过来了。并做了一点小小的改动。源码见下#include<windows.h>#include<math.h>#include<gl/GL.h>#include<gl/glut.h>intSCREEN_HEIGHT=480;intNUMPOIN... 继续阅读 >

2020
09-27

OpenGL画bezier曲线

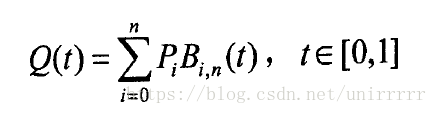BezierCurve算法是根据参数曲线方程来得到光滑曲线的一种算法，曲线方程的参数由控制点决定。其本质是由调和函数根据控制点插值而成，其参数方程如下：其中Pi（i=0,1，…，n）为控制点的向量，Bi,n(t)为伯恩斯坦Bernstein基函数，其多项式表示为：线性BezierCurve由两个控制点决定：二次BezierCurve由三个控制点决定：三次BezierCurve由四个控制点决定：如下图，t=AE:AB=BF:BC=CG:CD=EH:EF=FI:FG=HJ:HI，J即为Bez... 继续阅读 >

2020
09-27

OpenGL绘制Bezier曲线的方法

本文实例为大家分享了OpenGL绘制Bezier曲线的具体代码，供大家参考，具体内容如下项目要求：?使用鼠标在屏幕中任意设置控制点，并生成曲线?使用鼠标和键盘的交互操作实现对曲线的修改。项目总体介绍本项目利用Bezier曲线生成算法生成可由用户自定义的曲线。可实现核心功能如下：1、用户用鼠标左击屏幕任意处产生记录点。2、鼠标右击屏幕任意处由先前的任意个数记录点和其先后关系生成Bezier曲线。另有辅助输入功能：1、按键盘‘C... 继续阅读 >