分类：梯度下降

2021
02-21

利用Python实现最小二乘法与梯度下降算法

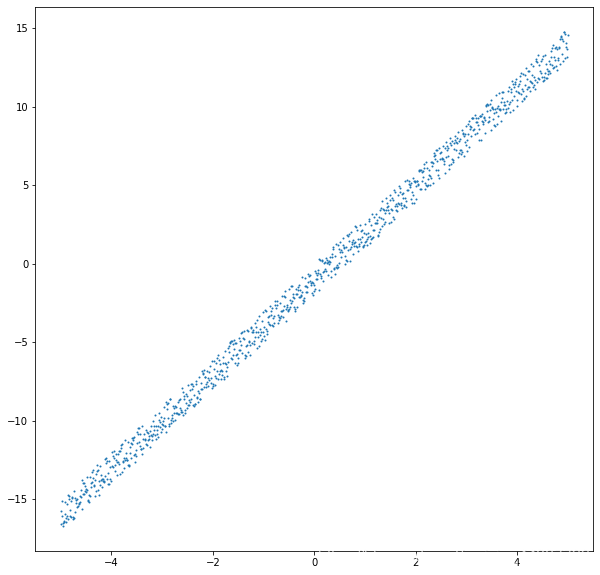导入所需库%matplotlibinlineimportsympyimportnumpyasnpimportmatplotlib.pyplotaspltfromsympy.abcimportxasa,yasb生成模拟数据#模拟函数y=3x-1#自变量x=np.linspace(-5,5,num=1000)#加入噪声noise=np.random.rand(len(x))*2-1#因变量y=3*x-1+noise查看所生成数据的图像plt.figure(figsize=(10,10))plt.scatter(x,y,s=1)求代价函数的偏导y=ax+b#目标函数e=1/2*Σ([axi+b]-yi)^2#代价函数，求使得代价函数... 继续阅读 >

2020
10-08

浅谈matplotlib 绘制梯度下降求解过程

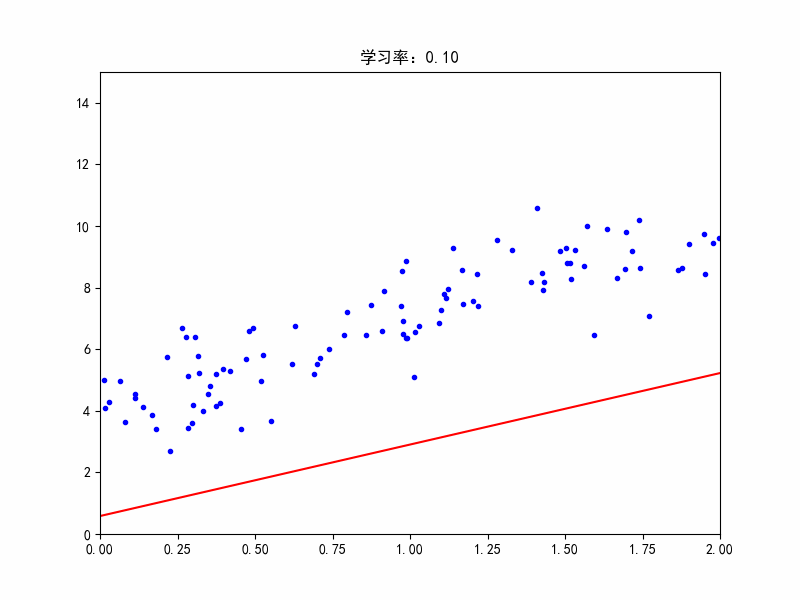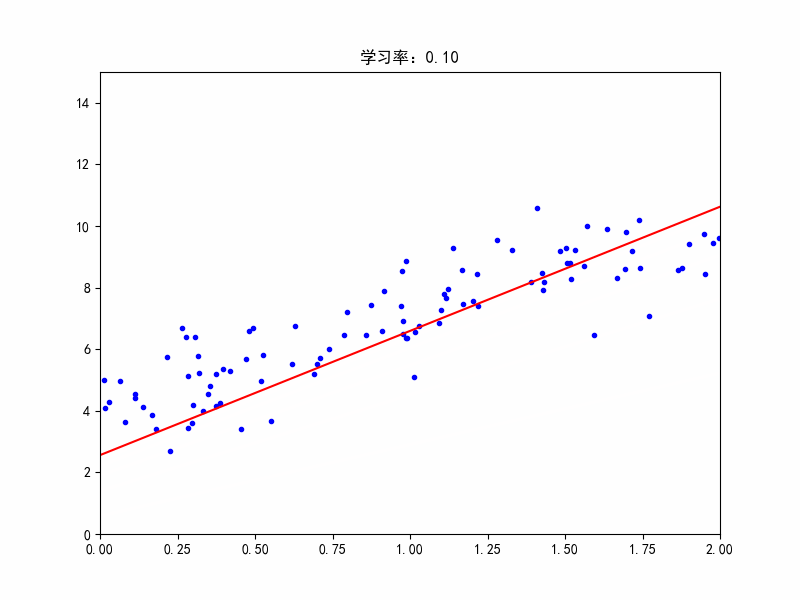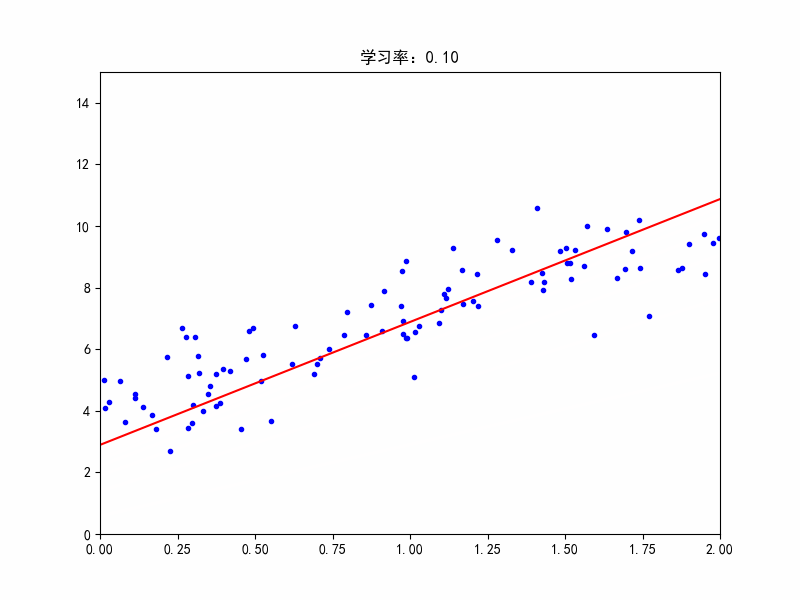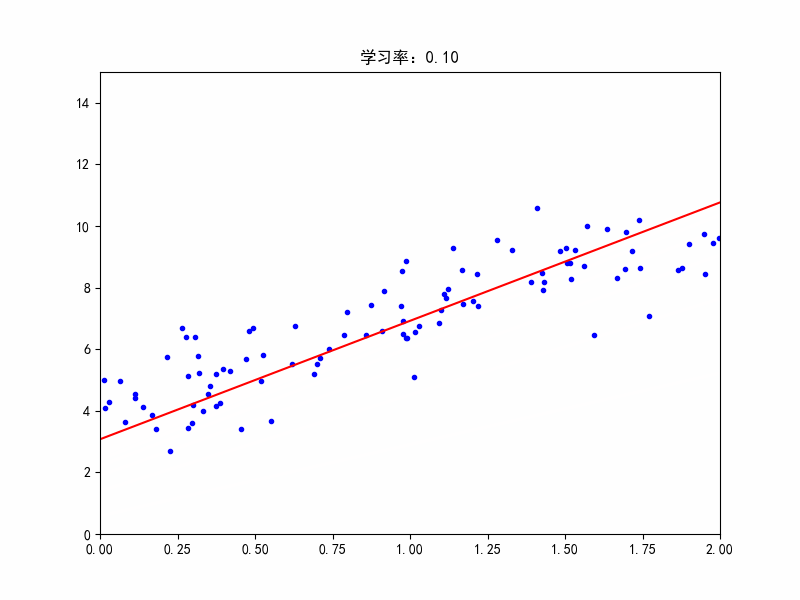机器学习过程中经常需要可视化，有助于加强对模型和参数的理解。下面对梯度下降过程进行动图演示，可以修改不同的学习率，观看效果。importnumpyasnpimportmatplotlib.pyplotaspltfromIPythonimportdisplayX=2*np.random.rand(100,1)y=4+3*X+np.random.randn(100,1)#randn正态分布X_b=np.c_[np.ones((100,1)),X]#c_行数相等，左右拼接eta=0.1#学习率n_iter=1000#迭代次数m=100#样本点个数theta=n... 继续阅读 >

2020
10-08

Keras SGD 随机梯度下降优化器参数设置方式

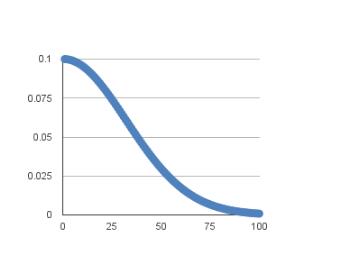SGD随机梯度下降Keras中包含了各式优化器供我们使用，但通常我会倾向于使用SGD验证模型能否快速收敛，然后调整不同的学习速率看看模型最后的性能，然后再尝试使用其他优化器。Keras中文文档中对SGD的描述如下：keras.optimizers.SGD(lr=0.01,momentum=0.0,decay=0.0,nesterov=False)随机梯度下降法，支持动量参数，支持学习衰减率，支持Nesterov动量参数：lr：大或等于0的浮点数，学习率momentum：大或等于0的浮点数，动... 继续阅读 >

2020
09-25

python使用梯度下降和牛顿法寻找Rosenbrock函数最小值实例

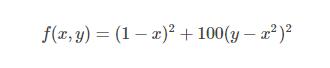Rosenbrock函数的定义如下：其函数图像如下：我分别使用梯度下降法和牛顿法做了寻找Rosenbrock函数的实验。梯度下降梯度下降的更新公式：图中蓝色的点为起点，橙色的曲线（实际上是折线）是寻找最小值点的轨迹，终点（最小值点）为(1,1)(1,1)。梯度下降用了约5000次才找到最小值点。我选择的迭代步长α=0.002α=0.002，αα没有办法取的太大，当为0.003时就会发生振荡：牛顿法牛顿法的更新公式：Hessian矩阵中的每一个二阶偏导... 继续阅读 >

2020
09-24

python实现梯度下降和逻辑回归

本文实例为大家分享了python实现梯度下降和逻辑回归的具体代码，供大家参考，具体内容如下importnumpyasnpimportpandasaspdimportosdata=pd.read_csv("iris.csv")#这里的iris数据已做过处理m,n=data.shapedataMatIn=np.ones((m,n))dataMatIn[:,:-1]=data.ix[:,:-1]classLabels=data.ix[:,-1]#sigmoid函数和初始化数据defsigmoid(z):return1/(1+np.exp(-z))#随机梯度下降defStocgrad_descent(... 继续阅读 >