分类：矩阵乘法

2021
04-27

Python实现求解斐波那契第n项的解法(包括矩阵乘法＋快速幂)

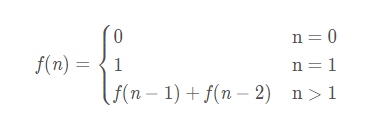斐波那契数列首先我们来定义一下斐波那契数列：即数列的第0项：算法一：递归递归计算的节点个数是O(2ⁿ)的级别的，效率很低，存在大量的重复计算。比如：f(10)=f(9)+f(8)f(9)=f(8)+f(7)重复8f(8)=f(7)+f(6)重复7时间复杂度是O(2ⁿ),极慢defF1(n):ifn<=1:returnmax(n,0)#前两项returnF1(n-1)+F1(n-2)#递归算法二：记忆化搜索开一个大数组记录中间结果，如果一个状态被计算过，则直... 继续阅读 >

2021
03-23

numpy和tensorflow中的各种乘法(点乘和矩阵乘)

点乘和矩阵乘的区别： 1)点乘(即“*”)----各个矩阵对应元素做乘法若w为 m*1 的矩阵，x为 m*n 的矩阵，那么通过点乘结果就会得到一个 m*n 的矩阵。若w为 m*n 的矩阵，x为 m*n 的矩阵，那么通过点乘结果就会得到一个 m*n 的矩阵。w的列数只能为 1 或 与x的列数相等(即n)，w的行数与x的行数相等 才能进行乘法运算。2)矩阵乘----... 继续阅读 >

2021
03-22

NumPy 矩阵乘法的实现示例

NumPy支持的几类矩阵乘法也很重要。元素级乘法你已看过了一些元素级乘法。你可以使用multiply函数或*运算符来实现。回顾一下，它看起来是这样的：m=np.array([[1,2,3],[4,5,6]])m#显示以下结果：#array([[1,2,3],#[4,5,6]])n=m*0.25n#显示以下结果：#array([[0.25,0.5,0.75],#[1.,1.25,1.5]])m*n#显示以下结果：#array([[0.25,1.,2.25],#[4.,6.25,9.]])np.multiply(m,n)#相当于... 继续阅读 >

2021
01-21

C++ 利用硬件加速矩阵乘法的实现

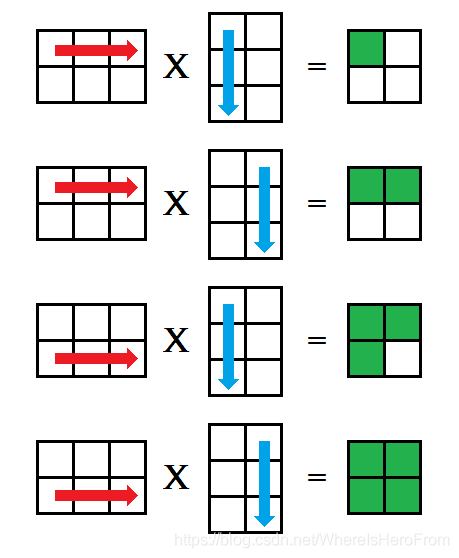一、矩阵乘法定义矩阵Ax×y和矩阵Bu×v相乘的前提条件是y==u，并且相乘后得到的矩阵为Cx×v（即A的行和B的列构成了矩阵C的行列）； 二、矩阵类封装我们用C++封装了一个n×m的矩阵类，用二维数组来存储数据，定义如下：#defineMAXN1000#defineLL__int64classMatrix{private:intn,m;LL**pkData;public:Matrix():n(0),m(0){pkData=NULL;}voidAlloc(){pkData=newLL... 继续阅读 >